Billiard dynamics under gravity

Question

Has the dynamics of billiards in a polygon subject to gravity been studied? What I have in mind is something like this:
          
Still Snell's Law applies so the angle of incidence equals the angle of reflection, and the collision is perfectly elastic, but the path followed by the ball between contacts is a parabola. I am wondering if such a system can somehow be converted into one without gravity, so that our understanding of, e.g., the dynamics of billiards in a square may be applied.

To be specific:

What initial conditions lead to a periodic path in a square?

For example, suppose the square has corners $(0,0)$ and $(1,1)$. Starting at $p_0=(0,\frac{1}{2})$, with vertical velocity zero and horizontal velocity that first lands the ball at $p_1=(\frac{1}{2},0)$ (say, $v_x=\frac{1}{2}$, gravity $=1$), produces (I believe) a periodic path bouncing between the three points $\{ p_0, p_1, p_2 \}$, where $p_2=(1,\frac{1}{2})$:
                    
I'd appreciate literature pointers—Thanks!

---

Addendum. Following fedja's intriguing comment, here a path when gravity is tilted $30^\circ$:
      

Answer 1

Here is the rather interesting result I get in Maple for a square of side 1 tilted at 30 degrees, acceleration of gravity = 1, initial position at the top left corner and moving horizontally with speed 1. This plot goes up to $t=300$. The trajectories appear to fill up a rectangular region (the top right boundary being an envelope).

EDIT: And here's one with two envelopes, each parallel to an axis of the square.

Answer 2

As fedja notes in the comments, the bounces off the right and left walls can be accounted for by unfolding the unit square into a horizontal strip, so the trajectories can be viewed as the parabolic arcs of an elastic ball that bounces off a floor and is constrained by a ceiling. We may as well start things at (0,0).

If the bouncing ball doesn't hit the ceiling -- say it maxes out at $(a,h)$ with $0 < h < 1$ -- then it simply traces a repeating set of parabolic arcs in the horizontal strip, with periodicity $2a$, in which case the billiard trajectory in the unit square is periodic if and only if $a$ is rational.

If the bouncing ball does hit the ceiling, say at $(a,1)$, then the trajectory thereafter is simply the reflection of the initial parabolic arc across the vertical line $x=a$. This again results in a repetition of arcs with period $2a$, so in either case (hitting the ceiling or not), the billiard trajectory in the unit square is periodic if and only if $a$ is rational.

The general case -- starting at an arbitrary point with an arbitrary initial speed and direction -- can be easily handled by following the initial parabolic arc to or from the floor and to or from its vertex or the ceiling, whichever is lower.

Answer 3

Nice picture, Robert. I think the way to understand this is the following: Unfold the square to the plane, keeping track of the "new" direction of gravity each time you do a reflection. In my picture, the direction of the gravitational field in each square is given by the black arrow. Now we need to understand the trajectory of a particle subject to this field. I've sketched (freehand and poorly!) the start of a trajectory in red. This gives us an explanation for the "boundary" in Robert's picture: since the vertical component of the gravitational force is constant along a horizontal strip and symmetric in the line going horizontally down the middle of my picture, if we start off with not too much vertical velocity, we'll never get higher than a given horizontal line (dotted, blue) or lower than the reflection of that line in the reflected squares. http://www.freeimagehosting.net/newuploads/a772c.png

Edit: picture didn't go up the first time. Giving it another shot

Answer 4

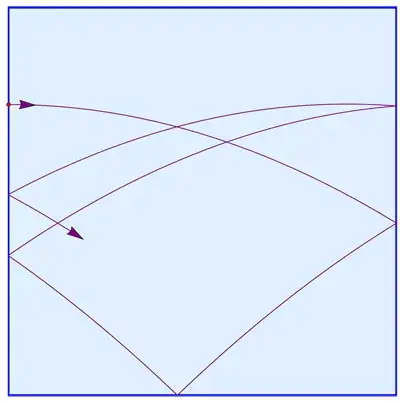
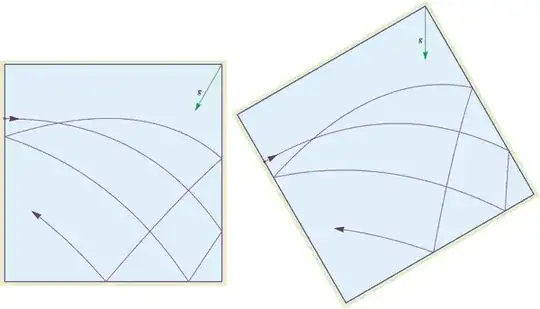
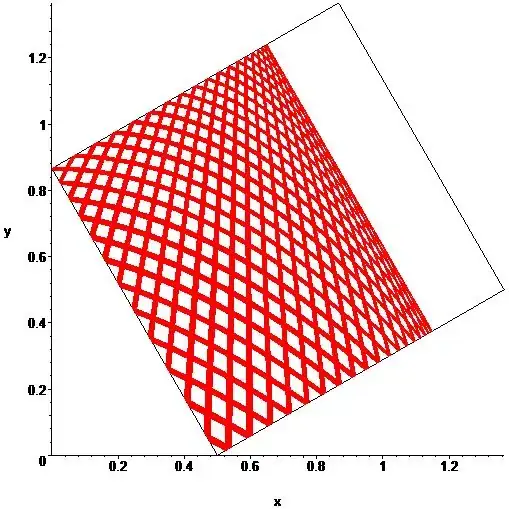
As Willie Wong pointed out early on in the comments to the original problem, conservation of energy applies to the billiard ball in the tilted (or untilted) square, and this in itself can prevent the ball from ever passing through certain points. In her answer analyzing Robert Israel's picture, Katie Mann expands on this. Let me try to flesh things out further.

It's worth viewing the billiard trajectory as taking place in the four copies of the unit square comprising the lefthand half of Katie's picture, with the four different directions for gravity. Let's think of this as the "Unit Square" $[-1,1]\times[-1,1]$ (as distinct from the "unit square" $[0,1]\times[0,1]$), with gravity vectors $(\pm\cos\theta,\pm\sin\theta)$, where $\theta = \pi/6$ and the signs are chosen for the quadrants so that gravity points generally toward the origin (i.e., toward the $x$ and $y$ axes). In this setting we can use toroidal boundary conditions instead of reflections to follow trajectories.

In his clarification of Katie's answer, Robert notes that the "$y$ component of energy" in the Unit Square is conserved. This holds for the "$x$ component" as well. This means that the two components of motion are completely independent! And this means that each component is simply described, as in my answer to the original problem (for the untilted square), by a repeating sequence of quadratic functions of time, each with its own period. Whether the overall billiard trajectory is periodic depends only on whether the ratio of these two periods is rational.

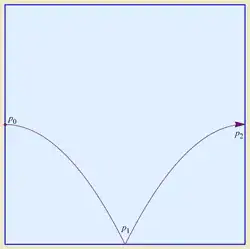
Robert's trajectory can be viewed as starting at $(-1,0)$ in the Unit Square with initial velocity $(\sin\theta,\cos\theta)$ subject to gravity vector $(\cos\theta,-\sin\theta)$. This means the $y$ component of the motion is described (initially) by

$$y(t)=t\cos\theta - (1/2)t^2\sin\theta$$

which maxes out when $t=\cos\theta/\sin\theta = \sqrt3$ (with $y(\sqrt3)=(6-3\sqrt3)/4 < 1$, so that, as Katie observed, the $y$ component of the trajectory never hits its "ceiling"). Thus the $y$ component in the Unit Square has period $4\sqrt3$.

The $x$ component, on the other hand, starts out from its "ceiling" heading toward its "floor" with equation

$$x(t) = -1 + t\sin\theta + (1/2)t^2\cos\theta$$

so that it completes half its cycle when

$$t = {\sqrt{\sin^2\theta + 2\cos\theta}-\sin\theta \over \cos\theta} = {\sqrt{1+4\sqrt3}-1 \over \sqrt3}$$

The ratio of the two periods, therefore, is $(\sqrt{1+4\sqrt3}-1)/2$, a decidedly irrational number. (Indeed, the ungainliness of this result makes me worry I've made a mistake somewhere in the algebra. Someone should doublecheck my work in any event, and please correct me if I'm wrong.) The irrationality of the ratio implies that Robert's trajectory is non-periodic.

It's worth considering what happens if one simply lets a billiard ball drop from the topmost point of the tilted square. This is equivalent to starting with zero velocity from $(-1,1)$ in the Unit Square, and in this case each component goes from its respective "ceiling" to "floor" and back, with equations

$$x(t) = -1 + (1/2)t^2\cos\theta$$ and $$y(t) = 1 - (1/2)t^2\sin\theta$$

which makes the ratio of the two components' periods equal to $\tan\theta$. For $\theta = \pi/6$ this is irrational, implying this trajectory is also non-periodic, but for other values of $\theta$, of course, the ratio can be rational. In particular, if you take the square on the hypotenuse of a right rational triangle (with the other two sides horizontal and vertical), and drop a billiard ball from its uppermost corner, the resulting trajectory will be periodic.

I hope I haven't gotten too much wrong here.

Correction (added August 3): In addition to the minor error Joseph O'Rourke pointed out in the comments, I was utterly wrong in what I said about right rational triangles. That's because the ratio of the periods for a ball dropped from the upper corner of a tilted square is $\sqrt{\tan \theta}$, not $\tan\theta$. There are certainly $\theta$'s for which $\sqrt{\tan\theta}$ is rational, but none of them come from right rational triangles, as that would violate Fermat's proscription on solutions to the equation $a^4 + b^4 = c^2$.

Answer 5

This is not an answer to the specific question asked, but I cannot resist sharing this with you.

There is a beautiful result of Chernov and Dolgopyat, see http://www-users.math.umd.edu/~dmitry/galton11new.pdf , on the billiard in Galton's board in the presence of gravity. The Galton board is a well-known device indended to reproduce the binomial distribution (see, e.g., http://mathworld.wolfram.com/GaltonBoard.html).

Chernov and Dolgopyat studied the situation when the board is extended periodically and indefinitely. Collisions with the obstacles are assumed elastic, so that no loss of energy occurs. The result is that despite the fact that gravity is directed down, the ball or particle will eventually reach the same horizontal level as it is at initially. Moreover, it reaches a small neighborhood of its initial state infinitely many times. This happens for a.e. initial condition.

Answer 6

This problem is very similar to what is known in the physics literature (including in real atom-optics experiments) as the "wedge billiard."

Self-edit: Another comment -

Formulas for linear stability of billiards with potentials (such as gravity) are given in Holger Dullin's paper here:

Holger R Dullin, "Linear stability in billiards with potential." Nonlinearity, Volume 11, Number 1, 11, 151. 1998.

Abstract: A general formula for the linearized Poincaré map of a billiard with a potential is derived. ...