In the paper, "Dissection with the Fewest Pieces is Hard, Even to Approximate" (arXiv, doi) by Bosboom et al., they write:
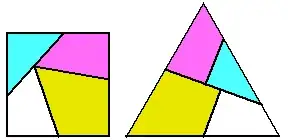
We have known for centuries how to dissect any polygon $P$ into any other polygon $Q$ of equal area, that is, how to cut $P$ into finitely many pieces and re-arrange the pieces to form $Q$. But we know relatively little about how many pieces are necessary. For example, it is unknown whether a square can be dissected into an equilateral triangle using fewer than four pieces. [emphasis added]
The authors seem to be knowledgeable about the subject, so I'd be inclined to trust their claim. As I mentioned in another MO answer, they point out that more generally, it is not known if "$k$ piece dissection," the problem of deciding whether two given polygons (say with rational vertices) admit a common dissection into at most $k$ pieces, is decidable. The trouble is that even if you restrict yourself to cuts that are piecewise-linear, there is no known a priori upper bound on how many "zigs and zags" a cut might have to take.