Is it possible to capture a sphere in a knot?

I would try to "gift wrap" the sphere. Take the 1-skeleton of the octahedron, and take an Eulerian path. Then make each vertex into a twist, and pull tight, so that it looks like the union of three orthogonal great circles. I have no idea though whether this has any length decreasing deformations. Here's a crude stereographic projection, teased apart so you can see the crossings:

See lower left Japanese glass float:

There's some variations one could make to this construction, if this doesn't work. Something like this:

Edit: Actually, I just realized that this won't work. One may deform the 1-skeleton of the octahedron by rotating both great circles toward the 3rd without changing length. So you can rotate the whole thing onto a great circle, then slip it off. The Japanese get around this issue by tying little knots where the strands clasp each other, which prevents the verices from moving. But of course this isn't allowed in the formulation of the problem.

Edit: I think the answer is "no". I found this abstract at Mathscinet, although I haven't looked up the article. Pronin proves that a (locally) minimal 1-complex (network) on a sphere is unstable. Since a piecewise linear "knot" on the surface of a sphere has underlying space a (multi) graph, one can deform the graph to decrease length, and the length of the knot decreases. The only thing I'm not quite sure about is whether Pronin allows multiple edges, but I'd be willing to bet that the same argument (whatever it is) works in this case.

Edit: This solution is incorrect, but I'm leaving it here because I think it's still interesting.

Here's a solution Scott Morrison and I came up with.

Choose a trivalent graph on the sphere with the vertices connected by segments of great circles such that any slight perturbation of the vertices would result in an a greater total edge length. The really symmetric tetradodecahedron on the sphere is such a graph.^† Now replace each vertex with a "clove hitch vertex" and each edge by a pair of strands:

Introduce some twists along the edges in order to make the whole link into a single knot. Two strands running between a pair of vertices can't be separated without making them longer, so the only way to deform the knot-around-the-sphere is to deform the "underlying graph", and we've chosen the graph so that any deformation would result in strictly larger total edge length.

The end result (without the twists to make a single component) would look like this if you used a tetrahedron instead:

^†If you don't believe that the symmetric tetrahedron is minimal in this way, either prove it in another answer, or ask another question! Edit: As some of you have pointed out, the tetrahedron is not such a minimal graph, and we were being too greedy asking for a minimal graph where the vertices are so far apart. So you have to find some graph which actually is minimal. I think a dodecahedron should do the trick (edit: it doesn't), but I don't know how to prove it.

The regular dodecahedron is not a local minimum for total edge length either. Consider the five vertices V_i, i = 1, ..., 5 of a face together with the "center" C of the face. The spherical triangle CV₁V₂ has angles 72°, 60°, 60°, so V₁V₂ > CV₁. Therefore if we move all five of the V_i to C, the total edge length decreases. (This part would be true even if the edges joining the V_i to the rest of the dodecahedron did not extend to pass through C, by the triangle inequality.)

As we move the V_i symmetrically towards C along the edges CV_i at constant speed, the total edge length is some smooth function which is smaller at the end of the motion than at the beginning. I want to prove the beginning is not a local minimum. If it were, there would be a second critical point in the interior of the motion. But that contradicts Torricelli's theorem—the angle CV₁V₂, which is 180° minus the angle between two of the edges incident on V₁, is decreasing during the motion, and thus only once equal to 60°.

Some "climber's intuition" suggested that it might be possible to do this with an ellipsoid. The idea is to tie two clove hitches near the pointy ends:

   alt text http://img.skitch.com/20091208-mch2jh1ufhc4r56puh8b5rfwh4.jpg

This doesn't seem to quite work -- either clove hitch can move towards the centre and simultaneously loosen. Maybe it's possible to get the ellipsoid just right so that it's "pointy enough the clove hitches can't fall off the end", and "round enough that the clove hitches can't loosen fast enough".

Even better, after looking at this, Anton and I realised that you can build "trivalent vertices" essentially using a clove hitch. He's about to post a followup answer explaining that geodesic trivalent graphs can be realised by "tight" knots.

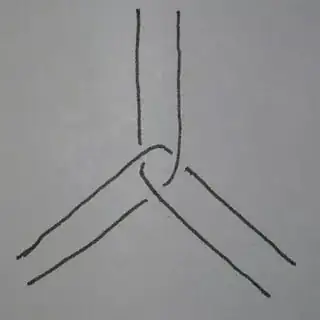
Well, here's a proof that the symmetric tetrahedron is not a local minimum - in fact, I claim that it's basically a local maximum!

Fix the positions of three of the vertices $v_1$, $v_2$, $v_3$ of the symmetric tetrahedron. First, let's find the point $p$ on the sphere for which the sum of the lengths of geodesics connecting $p$ to $v_1$, $v_2$, $v_3$ is minimal. By Torricelli's Theorem, this point must either be one of $v_1$, $v_2$, $v_3$, or a point where all edges leaving it meet at $120$ degrees. Thus, $p$ is one of $v_1$, $v_2$, $v_3$, the fourth vertex of the symmetric tetrahedron, or the antipodal point to one of the four points I already mentioned. By direct calculation, we see that $p$ is the antipodal point to the fourth vertex of the symmetric tetrahedron.

Now if we move the fourth vertex to any point $q$ nearby, and draw three great semicircles connecting it to the antipodal point $q'$ and passing through the other three vertices of the symmetric tetrahedron, we see that the sum of the lengths from $q$ is three pi minus the sum of the lengths from $q'$. Since the sum of the lengths from $q'$ is at least the sum of the lengths from $p$, the sum of the lengths from $q$ is at most the sum of the lengths from the top vertex of the symmetric tetrahedron. Thus, we can basically move the top vertex anywhere we like without increasing the total length of the string.

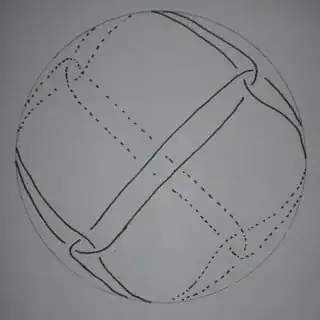
The next thing you will probably be tempted to try is the symmetric cube (using the same trick to handle the vertices of degree three). In this case, each vertex actually is at a strict local minimum if you hold the other vertices fixed. However, I'm pretty certain that it's possible to move all four vertices on the top face simultaneously either to the top of the sphere or to the equator of the sphere without increasing the total length during the process.

Edit: Here's a proof that we can move the vertices on the top face of the cube all upwards or downwards without increasing the total length. Let $x$ be the angle that the line connecting a vertex on the top face to the center of the sphere makes to the plane through the equator of the sphere. We are going to calculate the total length of all string above the equator as a function of $x$ - it's going to be $4x + 4(\mbox{angle between adjacent vertices})$. The dot product of the vectors corresponding to adjacent vertices is $\sin^2(x) = \frac{1-\cos(2x)}{2}$. Letting $a = \cos(2x)$, we see that the total length above the equator is $2\arccos(a) + 4\arccos(\frac{1-a}{2})$. Thus, since $\arccos$ is a concave function for $a$ between $0$ and $1$, that total length achieves its maximum when $a = \frac{1-a}{2}$, i.e. $cos(2x) = a = \frac{1}{3}$, which is the initial angle we started out with on the cube.

Adding to Zeb's proof that the tetrahedron can be deformed, one should notice that any tassellation of the sphere containing at least one hexagon (fullerene type) won't be rigid either. In fact already in the plane the regular hexagon can be inflated (at the expense of the 6 outgoing rays) with no change in total length, much more so on a positively curved surface. Like Zeb, I'm also skeptical about the cube. Perhaps the dodecahedron has a chance, since its pentagons are quite a bit flatter than the faces of either the cube or tetrahedron (but then the inflation procedure is also cheaper than for the triangle or the square).

I think the sphere cannot be removed. I think that in physical knot theory that is knot theory with constraints on quantities as length and thickness there are models where a quantity called entanglement is related to the curvature of the containing sphere. So in this case any transformation would have to be within a certain distance of the sphere. I suspect that this is enough to keep the sphere locked in. Here is a paper on knot theory that deals with entanglement:

http://rspa.royalsocietypublishing.org/content/468/2148/4024

Since Anton's beautiful solution makes use of the symmetry of the sphere, I wonder how similar results could be proven, or counterexamples given, for any other convex shape, including 2-dimensional ones - i.e. infinitely thin 3-dimensional objects. I can't figure a way to tie a cube or a square, but it seems that an equilateral triangle could be tied by 3 connected loops starting from some knot at the center and going over each vertex (forming 3 equilateral triangles 1/3 the size of the original).

(I would have liked to just leave this post as a comment to Anton's proof, but I'm not allowed to do that. Should it perhaps be a new question?)

It seems that both the 2-agon and the octahedron (which after all is a collection of 3 somewhat constrained 2-agons) can be shrunk off the sphere, but with 0 derivative at the start, which means that they come close. Perhaps the icosahedron could work (as for tying 5 edges into one vertex, a tangle of simple knots should do). But notice that inflating a triangle (even though it's fairly flat on an icosahedron) will trade off with shrinking not 3 (tetrahedron) or 6 (octahedron) other edges, but 9 of them. Such trade off would increase the total length on a plane, but on the sphere it depends on the curvature, i.e. the size of the triangles (similarly to what I pointed out re. the dodecahedron in an earlier post).

I suspect the just like no hexagon at all can be allowed on a graph tessellating the sphere, so no square or pentagon can be allowed to belong to any vertex other than a 3-edged one. If that's the case, probably the cube (which no one seems to have ruled out yet), icosahedron and dodecahedron are the only candidates for graphs with strictly locally minimal total length.

Other tessellations of the sphere with mixed polygons probably shouldn't work either. For example, considering a spherical triangular prism (2 squares and a triangle meeting at each of the 3 vertices): while inflating a triangle is harder than on a spherical tetrahedron, inflating a square will be easier than on a spherical cube (whose square is less curved). Similarly for a pentagonal prism: advantageous from the point of view of its 5 squares, but not from that of its 2 pentagons (when compared with the dodecahedron).

Very nice problem!

Reid, excellent proof. It works for the cube too and even kills the icosahedron. In this last case I don't know what the angles of a triangle are exactly, so let's just say 60+ each. Then joining each vertex to the center gives smaller triangles with 120, 30+ and 30+ degree angles and it's then clear that shrinking a triangle towards its center will again reduce the total length. More generally, your idea seems to kill the possibility any small enough face with 3, 4 or 5 edges, and one of those is certainly needed somewhere! My bet is now confidently on the sphere always escaping.