First, there is a great survey of locally convex topological spaces in section 424 of the Encyclopedic Dictionary of Mathematics. (The EDM, if you have not seen it, is a fabulous reference for all kinds of information. Even though we all have Wikipedia, the EDM is still great.) At the end it has a chart of many of these properties of topological vector spaces, indicating dependencies, although not all of them. This chart helped me a lot with your question. On that note, I am not a functional analyst, but I can play one on MO. Maybe a serious functional analyst can give you a better answer. (Or a worse answer? I wonder if to some analysts, everything is the machine.)
Every important topological vector space that I have seen in mathematics (of those that are over $\mathbb{R}$ or $\mathbb{C}$) is at least a Banach space, or an important generalization known as a Frechet space, or is derived from one of the two. We all learn what a Banach space is; a Frechet space is the same thing except with a countable family of seminorms instead of one norm. Many of the properties that you list, for instance metrizable and bornological, hold for all Frechet spaces. In emphasizing Banach and Frechet spaces, the completeness property is implicitly important. Since a normed linear space is a metric space, you might as well take its completion, which makes it Banach. A Frechet space is a generalization of a metric space known as a uniform space and you might as well do the same thing. Also the discussion is not complete without mentioning Hilbert spaces. You can think of a Hilbert space either as a construction of a type of Banach space, or a Banach space that satisfies the parallelogram law; of course it's important.
Of the properties that do not hold for all Frechet spaces, I can think of four that actually matter: reflexive, nuclear, separable, and unconditional. In addition, a Schwartz space isn't really a space with a property but a specific (and useful) construction of a Frechet space. (Edit: It seems that "Schwartz" means two things, the Schwartz space of rapidly decreasing smooth functions, and the Schwartz property of a locally convex space.)
A discussion of the properties that I think are worth knowing, and why:
reflexive. This means a space whose dual is also its pre-dual. If a Banach space has a pre-dual, then its unit ball is compact in the weak-* topology by the Banach-Alaoglu theorem. In particular, the set of Borel probability measures on a compact space is compact. This is important in geometry, for sure. Famously, Hilbert spaces are reflexive. Note also that there is a second important topology, the weak-* topology when a pre-dual exists, which you'd also call the weak topology in the reflexive case. (I am not sure what good the weak topology is when they are different.)
separable. As in topology, has a countable dense subset. How much do you use manifolds that do not have a countable dense subset? Inseparable topological vectors are generally not that useful either, with the major exception of the dual of a non-reflexive, separable Banach space. For instance $B(H)$, the bounded operators on a Hilbert space, is inseparable, but it is the dual of the Banach space of trace-class operators $B_1(H)$, which is separable.
unconditional. It is nice for a Banach space to have a basis, and the reasonable kind is a topological basis, a.k.a. a Schauder basis. The structure does not resemble familiar linear algebra nearly as much if linear combinations are only conditionally convergent. An unconditional basis is an unordered topological basis, and an unconditional space is a Banach space that has one. There is a wonderful structure theorem that says that, up to a constant factor that can be sent to 1, the norm in an unconditional space is a convex function of the norms of the basis coordinates. All unconditional Banach spaces resemble $\ell^p$ in this sense. Note also that there is a non-commutative moral generalization for operators, namely that the norm be spectral, or invariant under the available unitary group.
nuclear. Many of the favorable properties of the smooth functions $C^\infty(M)$ on a compact manifold come from or are related to the fact that it is a nuclear Frechet space. For instance, in defining it as a Frechet space (using norms on the derivatives), you notice that the precise norms don't matter much. This doesn't necessarily mean that you should learn the theory of nuclear spaces (since even most analysts don't). But in drawing a line between constructions and properties, Opinion seems to be split as to whether the theory of nuclear spaces is tangential or fundamental. Either way, my impression is that the main favorable properties of $C^\infty(M)$ are that it is Frechet, reflexive, and nuclear. On the other hand, infinite-dimensional Banach spaces are never nuclear.
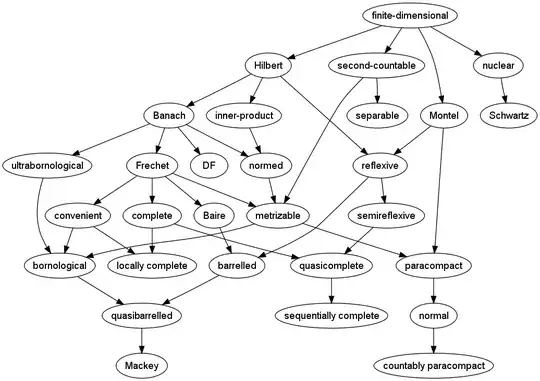
Prompted by Andrew's question, I compiled some data on relationships between types of locally convex topological spaces. In particular, I made a Hasse diagram (drawn with Graphviz) of properties included below. It began as a simplification of the one in EDM, but then I added more conditions. The rule for the Hasse diagram is that I only allow "single-name" properties, not things like Frechet and nuclear, although adverbs are allowed. The graph makes the topic of locally convex spaces look laughably complicated, but that's a little unfair. You could argue that there are more than enough defined properties in the field, but of course mathematicians are always entitled to make new questions. Moreover, if you look carefully, relatively few properties toward the top of the diagram imply most of the others, which is part of the point of my answer. If a topological vector space is Banach or even Frechet, then it automatically has a dozen other listed properties.
I have the feeling that the Hasse diagram has missing edges even for the nodes listed. If someone wants to add comments about that, that would be great. (Or it could make a future MO question.) The harder question is combinations of properties. I envision a computer-assisted survey to compare all possible combinations of important properties, together with citations to counterexamples and open status as appropriate. I started a similar computer-assisted survey of complexity classes a few years ago.