100

Is $$ \sum_{n=0}^\infty {x^n \over \sqrt{n!}} > 0 $$ for all real $x$? (I think it is.) If so, how would one prove this? (To confirm: This is the power series for $e^x$, except with the denominator replaced by $\sqrt{n!}$.)

J Russell
  • 1,103
  • 1
    you cannot argue form the exponential. This replacement change everything. Instead, use a software to plot the function; then you will be able to guess something. – Denis Serre Jan 05 '12 at 13:36
  • 35
    I don't know why people are voting to close this. I would be interested in learning about methods that could be used to prove that an entire function, given by convergent power series, had no real zeroes, so I would like this question to stay open. – David E Speyer Jan 05 '12 at 15:07
  • 1
    If your series has a real root $\rho$ then all the polynomials $\sum_{n=0}^{2k+1}x^n/\sqrt{n!}$ have a root in the interval $(\rho,0)$ for $k>\rho^2/2$. – Roland Bacher Jan 05 '12 at 15:09
  • 5
    I completely agree with @David. – Igor Rivin Jan 05 '12 at 15:33
  • 2
    On the other hand, it would be nice if the OP would provide some evidence for why this might be true. – Igor Rivin Jan 05 '12 at 15:34
  • 1
    I voted to close because the question is not motivated. The function seems to be monotone and have a positive limit as $x\to -\infty$. –  Jan 05 '12 at 15:51
  • @Mark: I believe this was the OP's motivation (I can't speak for him/her, of course), and removing the "seems" would be the interesting part. – Igor Rivin Jan 05 '12 at 16:07
  • 2
    @Igor: The question has infinitely many equally interesting modifications. Why is OP interested in $\sqrt(n!)$ and not in $(n!)^{1/3}$? The question by David Speyer above makes much more sense but it is a different question. –  Jan 05 '12 at 16:11
  • 7
    $1/\sqrt{n!}$ for the absolute value of coefficients is an interesting choice for random polynomials (called Weyl polynomials), their roots are roughly uniformly distributed in a large disc. – Roland Bacher Jan 05 '12 at 17:09
  • 27
    This is very far from a solution, but might be of interest. Let $F(x) = \sum_{n=0}^\infty x^n/\sqrt{n!}$ and let $H(x) = F(x)F(-x)$. Then $H(x) = \sum_{n=0}^\infty c_nx^n/\sqrt{n!}$ where $c_n = \sum_{r=0}^n (-1)^r \sqrt{\binom{n}{r}}$. It is clear that $c_n = 0$ if $n$ is odd, and it would be sufficient to prove that $c_n > 0$ if $n$ is even, since then $F(-x) = H(x)/F(x)$ is a positive function. I have checked this is true for $n \le 100$. – Mark Wildon Jan 05 '12 at 17:34
  • Call the function under discussion $\small exph(x)$ then the inverse of $\small logh(1+x)= inverse(exph(x)-1) $. The taylorseries for $\small logh $ may then be instructive for the question, whether $\small logh(0+\epsilon) \to -\infty $ for $\small \epsilon \to +0$ – Gottfried Helms Jan 05 '12 at 18:10
  • I do not really see hints for the solution of the current question, but for the interested a related question may be seen at http://math.stackexchange.com/questions/26425 – Gottfried Helms Jan 05 '12 at 18:17
  • @Roland: Your explanation for $\sqrt{n!}$ would make the question much better. –  Jan 05 '12 at 18:27
  • @Mark Wildon: Something is wrong. Maple says that for $n=66$ your sum $c_n$ is about $-15$. –  Jan 05 '12 at 19:15
  • 3
    @Mark Sapir: please could you check that Maple is using sufficient internal precision? I checked using Mathematica and Magma and they agree that $c_{66} = 0.099654081141578677146$ to 20 decimal places. – Mark Wildon Jan 05 '12 at 19:29
  • @Mark Wildon: You are right, with precision $10^{-40}$, all $c_n$, $n\le 200$, are positive (precision 20 is not enough for $n\ge 108$). –  Jan 05 '12 at 20:07
  • Maple agrees $c_{66} = 0.099654\dots$ – Gerald Edgar Jan 05 '12 at 20:15
  • @Mark Sapir: "what's special about square root" is a valid question, and I agree that the OP should elaborate why he asks the question. – Igor Rivin Jan 05 '12 at 20:19
  • @Igor: I don't have any compelling evidence that this conjecture is true (although I believe it is). My best evidence is straightforward numerical experimentation. Also, intuition leads me to think it's true, and when I get stuck trying to prove it it's because "this intermediate step doesn't seem to help much," rather than "this intermediate step seems not to be true." – J Russell Jan 05 '12 at 21:06
  • 1
    @Mark: Yes, I don't have any reason to believe that $\sqrt{n!}$ is any different than $(n!)^\alpha$, where $0 < \alpha < 1$ (although, hypothetically, $\alpha = {1 \over 2}$ might be an easier special case). – J Russell Jan 05 '12 at 21:07
  • @Gottfried: Thank you for pointing out the related math.stackexchange question (looking at $(n!)^\alpha$ for $\alpha \approx 2 > 1$. I did not realize that there was a connection to Bessel functions. – J Russell Jan 05 '12 at 21:07
  • Among other experiments, I tried computing this function with a reasonably large negative number $x=-2000$; after computing the sum of the first $10^7$ terms in the power series, I got a value $\approx 3.6132257... \times 10^{868571}$. This leads me to believe that the function might be positive. However, without a more careful asymptotic analysis, I cannot say more. – Suvrit Jan 05 '12 at 21:20
  • @Mark Wildon: I checked till 1000. The numbers $c_{2k}$ are slowly decreasing staying positive. Say, $c_{1000}=.01988031033713112805873543299436989059...$. It looks like you just discovered a new property of binomial coefficients. –  Jan 05 '12 at 21:30
  • 14
    @Mark Wildon You should really post that observation as a separate question, because it is absolutely bizarre that it works. The largest term in the sum defining $c_{1000}$ is about $1.4 \times 10^{300}$. The fact that you get such nice cancellation to get an answer near $0.02$ seems like a miracle to me. Of course, $\sum (-1)^r \binom{n}{r}$ has even larger terms cancelling, but that is for a very good reason; I can't see any reason for your sum to be so small. – David E Speyer Jan 05 '12 at 22:45
  • 1
    It seems that $\forall \alpha \in [0,1]$ $\sum_{k=0}^n (-1)^k \binom{n}{k}^{\alpha} \in [0,1]$ – Arthur B Jan 05 '12 at 23:00
  • @Arthur B: Yes, it is equal to 0 for $\alpha=1$ and seems to be increasing with $\alpha$ decreasing to $0$. Perhaps it is possible to show that the derivative with respect to $\alpha$ is negative. –  Jan 05 '12 at 23:11
  • For $\alpha=0$, the sum is 1. So the sum $\sum_{k=0}^n (-1)^k {n\choose k}^\alpha$ is monotonously decreasing from 1 to 0. –  Jan 05 '12 at 23:18
  • 2
    @David Speyer: As suggested, I have posted a new question about the behaviour of the alternating sum. – Mark Wildon Jan 06 '12 at 01:01
  • 1
    I agree that this question should not be closed. If it gets closed I will do everything to re-open it. – GH from MO Jan 06 '12 at 02:35
  • The answer to your question is affirmative, read my response below. – GH from MO Jan 06 '12 at 06:03
  • @Mark Sapir. This is plenty motivated. There are many problems in math research which reduce to a specific function being positive or increasing or convex or wherever. – Daniel Parry Oct 03 '15 at 16:45
  • @DanielParry the question now would be if there is one that reduces to this specific function being positive, which was about the point made by Mark Sapir if I understood correctly. But why restart that debate from almost four years ago. –  Oct 03 '15 at 17:25

8 Answers8

121

Looks like the computers really spoiled us :)

GH gave a perfectly valid answer already but the cheapest way to prove positivity is to write $\int_0^1(1-t^n)\log(\frac 1t)^{-3/2}\,\frac{dt}t=c\sqrt n$ with some positive $c$ (just note that the integral converges and the integrand is positive, and make the change of variable $t^n\to t$). Hence $\int_0^1 (f(x)-f(xt))\log(\frac 1t)^{-3/2}\,\frac{dt}t=cxf(x)$. If $x$ is the largest zero of $f$ (which must be negative), then plugging it in, we get $0$ on the right and a negative number on the left, which is a clear contradiction. Thus, crossing the $x$-axis is impossible. Of course, there is nothing sacred about $1/2$. Any power between $0$ and $1$ works just as well.

Mariano Suárez-Álvarez
  • 46,795
fedja
  • 59,730
  • 3
    Very slick! I had not seen that trick before. – David E Speyer Jan 06 '12 at 13:26
  • 4
    Fedja, thank you. Because $d e^x / dx = e^x$, you can show that $e^x$ is positive by asking what would happen at a zero crossing. I've tried (unsuccessfully) to analyze $f'(x)$ with the hope of doing something similar. Your proof strikes me as having the same flavor as that sort of manipulation. Could you offer any motivation for how you came up with your integral "operator"? – J Russell Jan 06 '12 at 14:35
  • Altogether, very nice. – J Russell Jan 06 '12 at 14:36
  • 2
    This is awesome!

    http://www.youtube.com/watch?v=b2RiI9v3io4

     – Liviu Nicolaescu Jan 06 '12 at 14:43
  • 24
    @ J Russell. Yes, I started with the proof for the exponent you mentioned. The main difference is that you need half-derivative here, not the full one. The half-derivative (or, rather, quarter-Laplace) operator is well-known: it is just (regularized) convolution with $|t|^{-3/2}$. We needed the one-sided version here (the other side is not integrable), which works especially well on the negative exponents: $\int_0^\infty \frac{e^{-nx}-e^{n(x+t)}}{t^{1/2}}\frac{dt}{t}=n^{1/2}e^{-nx}$, so I just made the logarithmic change of variable to make it act on powers as needed. – fedja Jan 06 '12 at 16:53
  • @fedja: Thank you, that's quite enlightening. – J Russell Jan 06 '12 at 18:57
  • Beautiful and educative – Yemon Choi Jan 06 '12 at 22:29
  • Beautiful indeed. I had the feeling that this idea might also lead to $\forall x\in\mathbb{R}:\sum_{r=0}^{2n}x^r{2n\choose r}^{1/2}>0$ (cf. http://mathoverflow.net/questions/85013/alternating-sum-of-square-roots-of-binomial-coefficients/). I could not make it work, but admittedly I have not tried too hard either. – GH from MO Jan 07 '12 at 02:38
  • 5
    Nice!! For what its worth, $c$ is $\int_0^\infty (1-e^{-x}) \phantom. dx^{3/2} = 2 \Gamma(1/2) = 2\sqrt{\pi}$ by integration by parts. [My previous comment, now deleted, reported an incorrect answer because I left the factor $1/t$ out of the integrand in the numerical calculation.] – Noam D. Elkies Jan 07 '12 at 23:02
  • 1
    Do you really think so? I don't. – fedja Jan 08 '12 at 15:59
  • Very nice answer, but I have more questions... How about the power series is defined on the complex plane? Can you show there is no zero point? – student Nov 19 '15 at 02:50
  • +1. Magical feat! Could you please explain the purpose of the expression $\frac{e^{−nx}−e^{n(x+t)}}{t^{\frac12}}\frac{dt}t=n^\frac12 e^{−nx}$ in your comment revealing your motivation for the setup? I suppose the reason you consider half-derivative as opposed to other power the power on $n$ is $\frac12$? If it is $n^a$, you will use $a$-derivative, right? – Hans May 18 '20 at 03:59
  • To be clear, I understand the integral involving $e^{-nx}$ quoted in my last comment transforms into your original integral. What I want to know is where and how this comes about or its motivation. – Hans May 18 '20 at 15:18
24

The affirmative answer follows from my response to this related question.

EDIT. Noam Elkies gave a nicer and more general argument here.

Community
  • 1
GH from MO
  • 98,751
17

Here is another non-answer. In "Asymptotic Methods in Analysis", chapter 6, de Bruijn proves that $$S(s,n)=\frac{2}{\pi}\Gamma(s)(2ns\log 2n)^{-s}\left(\sin(\pi s)+O\left((\log n)^{-1}\right)\right)$$ where $$S(s,n)= \sum_{k=0}^{2n} (-1)^k \binom{2n}{k}^s$$ for all $0\le s\le\frac{3}{2}$. So at least this explains things asymptotically.

Gjergji Zaimi
  • 85,056
11

Additional data for Liviu's plots. I used Pari/GP with 1200 digits dec prec, documenting also the required number of terms after which the absolute values of the summands of the series decrease below 1e-100. There seems to be no local minimum...

$\small \begin{array}{rl|r} & & \text{# of terms}\\ x & f(x) & \text{ required} \\ \hline \\ -1 & 0.438599896749 & 201 \\ -2 & 0.247539616819 & 201 \\ -3 & 0.162554775870 & 211 \\ -4 & 0.117399404501 & 257 \\ -5 & 0.0903120618145 & 304 \\ -6 & 0.0726061182760 & 354 \\ -7 & 0.0602796213492 & 407 \\ -8 & 0.0512783927864 & 464 \\ -9 & 0.0444561508357 & 525 \\ -10 & 0.0391295513879 & 589 \\ -11 & 0.0348689168813 & 658 \\ -12 & 0.0313919770798 & 730 \\ -13 & 0.0285063993737 & 808 \\ -14 & 0.0260770215882 & 889 \\ -15 & 0.0240063146159 & 976 \\ -16 & 0.0222222780410 & 1067 \\ -17 & 0.0206706877888 & 1162 \\ -18 & 0.0193099849974 & 1263 \\ -19 & 0.0181078191003 & 1369 \\ -20 & 0.0170386561852 & 1479 \\ -21 & 0.0160820905671 & 1595 \\ -22 & 0.0152216309789 & 1715 \\ -23 & 0.0144438135509 & 1841 \\ -24 & 0.0137375438980 & 1972 \\ -25 & 0.0130936024884 & 2108 \\ -26 & 0.0125042681404 & 2250 \\ -27 & 0.0119630281606 & 2396 \\ -28 & 0.0114643528377 & 2548 \\ -29 & 0.0110035182996 & 2705 \\ -30 & 0.0105764661081 & 2867 \\ -31 & 0.0101796910429 & 3035 \\ -32 & 0.00981015071575 & 3208 \\ -33 & 0.00946519223932 & 3386 \\ -34 & 0.00914249232841 & 3569 \\ -35 & 0.00884000806032 & 3758 \\ -36 & 0.00855593615550 & 3953 \\ -37 & 0.00828867911422 & 4152 \\ -38 & 0.00803681690505 & 4357 \\ -39 & 0.00779908317617 & 4567 \\ -40 & 0.00757434517200 & 4783 \\ -41 & 0.00736158670179 & 5004 \\ -42 & 0.00715989363457 & 5231 \\ -43 & 0.00696844149585 & 5462 \\ -44 & 0.00678648482039 & 5700 \\ -45 & 0.00661334797911 & 5942 \\ -46 & 0.00644841724806 & 6190 \\ -47 & 0.00629113392871 & 6444 \\ -48 & 0.00614098836080 & 6703 \\ -49 & 0.00599751469633 & 6967 \\ -50 & 0.00586028632445 & 7236 \\ -51 & 0.00572891185489 & 7511 \\ -52 & 0.00560303158255 & 7792 \\ -53 & 0.00548231436720 & 8078 \\ -54 & 0.00536645487311 & 8369 \\ -55 & 0.00525517112099 & 8666 \\ -56 & 0.00514820231209 & 8968 \\ -57 & 0.00504530688991 & 9275 \\ -58 & 0.00494626080983 & 9588 \\ -59 & 0.00485085599129 & 9907 \\ -60 & 0.00475889893049 & 10230 \\ -61 & 0.00467020945455 & 10560 \\ -62 & 0.00458461960073 & 10894 \\ -63 & 0.00450197260623 & 11234 \\ -64 & 0.00442212199624 & 11580 \\ -65 & 0.00434493075923 & 11931 \\ -66 & 0.00427027059992 & 12287 \\ -67 & 0.00419802126157 & 12649 \\ -68 & 0.00412806991028 & 13016 \\ -69 & 0.00406031057475 & 13388 \\ -70 & 0.00399464363573 & 13766 \end{array} $

Thomas Klimpel
  • 2,444
Gottfried Helms
  • 5,214
  • 1
  • 21
  • 36
  • Thanks for the table. After I wrote that there is a minimum I did some additional computations and I realized I was wrong. Your table suggests that the question is far form trivial. – Liviu Nicolaescu Jan 06 '12 at 00:13
  • 2
    Note again the amazing cancellation. To compute that −70 term, the largest term in the sum is $(70)^{70^2}/\sqrt{(70)^2!} \approx e^{70^2/2}$. – David E Speyer Jan 06 '12 at 00:23
  • This function is indeed miraculous. – Liviu Nicolaescu Jan 06 '12 at 00:57
  • 1
    Gottfried, thank you for the numerical evaluation. This is consistent with how I believe the series behaves and with the numerical calculations I have done, although I didn't have the tools to push it out anywhere near as far as you did. A comment and an open-ended question: Presumably one could use interval arithmetic to produce a computer-aided proof of positivity for some negative values of $x$. Suppose you could prove positivity down to some large negative value. How large in magnitude would that $x$ have to be for you to really believe, absent a proof, that the series is positive? – J Russell Jan 06 '12 at 01:50
  • @David Speyer: I'm wondering if the cancellation is more amazing / surprising than the cancellation that happens for the power series for $\exp(x)$ for large negative values of x. – Andreas Rüdinger Sep 13 '16 at 20:02
6

This comment serves to record a partial attempt, which didn't get very far but might be useful to others. Following a suggestion of Mark Wildon and Arthur B, define $$f_n(\alpha) := \sum (-1)^r \binom{n}{r}^{\alpha}.$$ This is zero for $n$ odd, so we will assume $n$ is even from now on.

Mark Wildon shows that it would be enough to show that $f_n(1/2) \geq 0$ for all $n$. It is easy to see that $f_n(0) = 1$ and $f_n(1)=0$. Arthur B notes that, experimentally, $f_n(\alpha)$ appears to be decreasing on the interval $[0,1]$. If we could prove that $f_n$ was decreasing, that would of course show that $f_n(1/2) > f_n(1) =0$.

I had the idea to break this problem into two parts, each of which appears supported by numerical data:
1. Show that $f_n$ is convex on $[0,1]$.
2. Show that $f'_n(1) < 0$.
If we establish both of these, then clearly $f_n$ is decreasing.

I have made no progress on part 1, but here is most of a proof for part 2. We have $$f'_n(1) = \sum (-1)^r \binom{n}{r} \log \binom{n}{r} = \sum (-1)^r \binom{n}{r} \left( \log(n!) - \log r!- \log (n-r)! \right)$$ $$=-2 \sum (-1)^r \binom{n}{r} \left( \log(1) + \log(2) + \cdots + \log (r) \right)$$ $$=-2 \sum (-1)^r \binom{n-1}{r} \log r.$$ At the first line break, we combined the $r!$ and the $(n-r)!$ terms (using that $n$ is even); at the second, we took partial differences once.

This last sum is evaluated asymptotically in this math.SE thread. The leading term is $\log \log n$, so the sum is positive for $n$ large, and $f'_n$ is negative, as desired. The sole gap in this argument is that the math.SE thread doesn't give explicit bounds, so this proof might only be right for large enough $n$.

This answer becomes much more interesting if someone can crack that convexity claim.

Community
  • 1
David E Speyer
  • 150,821
5

Here is a plot of

$$\frac{1}{100}\left(\sum_{k=0}^{16}\frac{x^k}{\sqrt{k!}}\right)$$

on the interval $[-4,0]$. (Above I added the terms up to degree $16$.)

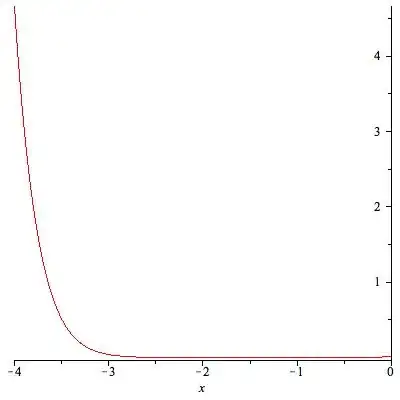
alt text

Next, is a plot of

$$\frac{1}{100}\left(\sum_{k=0}^{15}\frac{x^k}{\sqrt{k!}}\right)$$

on the interval $[-3,0]$. (Above I added the terms up to degree $15$)

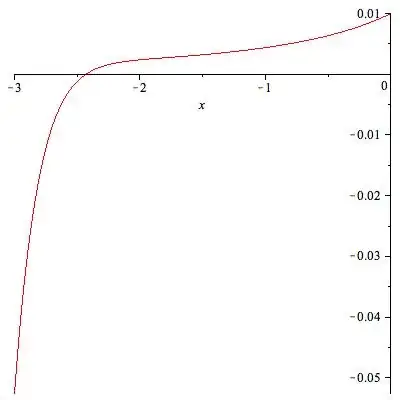
alt text

This is one strange series.

Community
  • 1
Liviu Nicolaescu
  • 34,003
  • Degree $n=16$ is of little use for $x=-10$, for example. The terms increase in size up to about $n=50$ and only then start to decrease. – Gerald Edgar Jan 05 '12 at 20:10
  • @Gerard I know that is why I chose shorter intervals. The function seems to have a local minimum at $-2.44$ and the value there is very small $\approx 0.202$. It's a curious function. – Liviu Nicolaescu Jan 05 '12 at 20:30
5

Another "not-yet-answer"...

I've tried another idea. Assume the function f(x) is expressed by the following composition: $$\small x' = \exp(x)-1 $$ $$\small f(x) = g(x') = g(exp(x)-1) $$ The idea is, that the unavoidable big "hump" in the partial sums, after which the sequence of partial sums begins to decrease, may be absorbed by the function $\small g(x)$ - because $\small \exp(x) $ is really small for large negative x and x' is then very little above -1. I did not yet arrive at a conclusive result; but the power series for $\small g(x) $ begins with the smooth looking form (and gives the partial sums for $\small x'=\exp(-100)-1 $):
$\qquad \small \begin{array} {r|r} \text{powerseries} & \text{partial sums for x' } \\ \hline \\ 1.00000000000 & 1.00000000000 \\ +1.00000000000x & 3.72007597602E-44 \\ +0.207106781187x^{2} & 0.207106781187 \\ +0.0344748426106x^{3} & 0.172631938576 \\ -0.0100670743762x^{4} & 0.162564864200 \\ +0.00821765977664x^{5} & 0.154347204423 \\ -0.00654357122833x^{6} & 0.147803633195 \\ +0.00537330847179x^{7} & 0.142430324723 \\ -0.00451702185603x^{8} & 0.137913302867 \\ +0.00386915976824x^{9} & 0.134044143099 \\ -0.00336528035075x^{10} & 0.130678862748 \\ +0.00296428202807x^{11} & 0.127714580720 \\ -0.00263893325448x^{12} & 0.125075647465 \\ +0.00237058888853x^{13} & 0.122705058577 \\ -0.00214611388717x^{14} & 0.120558944690 \\ +0.00195602261228x^{15} & 0.118602922077 \\ -0.00179331457091x^{16} & 0.116809607506 \\ +0.00165272361723x^{17} & 0.115156883889 \\ -0.00153022060566x^{18} & 0.113626663284 \\ +0.00142267593977x^{19} & 0.112203987344 \\ -0.00132762563657x^{20} & 0.110876361707 \\ +0.00124310598493x^{21} & 0.109633255722 \\ -0.00116753462507x^{22} & 0.108465721097 \\ +0.00109962364925x^{23} & 0.107366097448 \\ \end{array} $

The the question is, for some large negative x, say $\small x=-100 \qquad x'=exp(-100)-1 = -1+ \epsilon $ the series $\ g(x') $ converges to zero. Unfortunately - although we've translated the original problem to one with nice small numbers I don't see, how to really come nearer a solution, because the convergence of $\small g(-1+\epsilon) $ is really slow - if it converges at all to a positive value... So this is not yet a solution, but perhaps a suggestion for a path to try...

Thomas Klimpel
  • 2,444
Gottfried Helms
  • 5,214
  • 1
  • 21
  • 36
4

Although the following does not provide another proof (perhaps it is possible to attempt one on this basis) I found it nice to see the following pictures.
Let's take from the series $f(x) = \sum_{k=0}^\infty {x^k \over \sqrt{k!}}$ the following variants in the same spirit as we have the hyperbolic and trigonometric series from the exponential-series: $$\begin{array}{} \small \exp_{\tiny \sqrt{\,}}(x) &=& f(x) \\ \small \cosh_{\tiny \sqrt{\,}}(x) &=& \sum_{k=0}^\infty {x^{2k} \over \sqrt{(2k)!}} \\ \small \sinh_{\tiny \sqrt{\,}}(x) &=& \sum_{k=0}^\infty {x^{2k+1} \over \sqrt{(2k+1)!}} \\ \small \tanh_{\tiny \sqrt{\,}}(x) &=& { \sinh_{\tiny \sqrt{\,}}(x)\over \cosh_{\tiny \sqrt{\,}}(x) } \\ \small \cos_{\tiny \sqrt{\,}}(x) &=& \sum_{k=0}^\infty (-1)^k {x^{2k} \over \sqrt{(2k)!}} \\ \small \sin_{\tiny \sqrt{\,}}(x) &=& \sum_{k=0}^\infty (-1)^k {x^{2k+1} \over \sqrt{(2k+1)!}} \\ \end{array}$$ The answer to your question is equivalent to say, that always (="for real $x$")

  • $\small \cosh_{\tiny \sqrt{\,}}(x)$ is larger than $\small \sinh_{\tiny \sqrt{\,}}(x) $ $\qquad \qquad$ or that
  • $\small \mid \tanh_{\tiny \sqrt{\,}}(x) \mid \lt 1$

To illustrate this I've plotted the $\sinh_{\tiny \sqrt{\,}}$ and $\cosh_{\tiny \sqrt{\,}}$-curves:

bild1

This gives surely an extremely familiar impression...

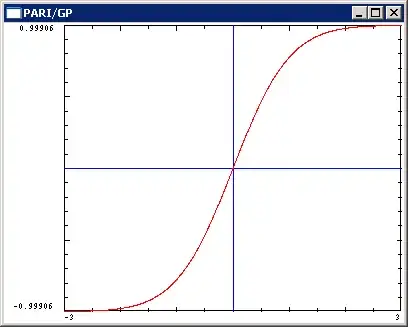
The $\tanh_{\tiny \sqrt{\,}}$-curve looks completely familiar too: bild2

and the image suggests, that indeed the absolute value of $\small \tanh_{\tiny \sqrt{\,}}(x) $ very likely is smaller than $1$ for all real $x$.

However, things are different for the $\sin_{\tiny \sqrt{\,}}$ and $\cos_{\tiny \sqrt{\,}}$ curves - they deviate strongly from the nicely periodic common trigonometric functions:

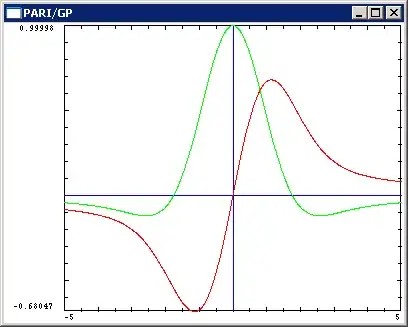
bild3

and combined they do not give a circle, but some ugly thing, strongly distorted (y-axis by $\small \cos_{\tiny \sqrt{ \,} }(\phi)$, x-axis by $\small \sin_{\tiny \sqrt{ \,} }(\phi)$, $\phi$ from $-5$ to $+5$) :

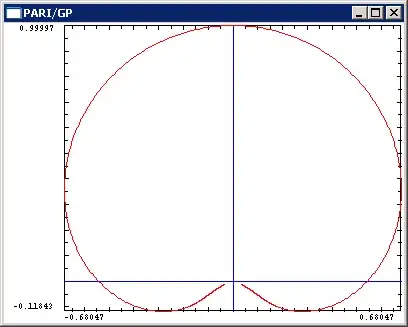
bild4

Gottfried Helms
  • 5,214
  • 1
  • 21
  • 36