Is the existence of electromagnetic standing waves dependent on the observers reference frame?

Question

If I take two plane EM waves travelling in opposite direction e.g. $E = E_0 \sin(kx-\omega t)$ and $E=E_0 \sin (kx + \omega t)$, they sum to give a standing wave with a time-averaged Poynting vector of zero.

If I use the appropriate special relativistic transformations to derive how these fields appear to an observer travelling at $v$ along the x-axis, I find that one E-field is diminished, one is boosted, whilst at the same time one wave is blue-shifted and the other red-shifted. These waves do not sum to give a standing wave in the moving frame of reference and have a non-zero time-averaged Poynting vector.

So, is the phenomenon of a standing wave dependent on the frame of reference of the observer?

Please note: That I have tried transforming the fields and summing them, but could not make sense of the result in terms of a travelling wave or a standing wave - hence the question. To get the bounty I'm looking for a form for $E^{\prime}$ or a decomposition of $E^{\prime}$ (that isn't just the sum of the transformed waves!) that makes clear the nature of the summed waves in the moving frame.

Answer 1

Yes, the concept of a standing wave is frame dependent, and a standing wave selects a specific frame just like the concept of a rest frame.

My initial answer was similar to BenCrowell's, and I made the same oversimplification mistake that his initial answer does. The are no spatial coordinates for the standing wave (even in its rest frame) in which the fields are a constant $\mathbf{E}=\mathbf{B}=0$. The existence of such would simplify the mental image of this scenario greatly, but unfortunately that is not the case.

However in the rest frame there are spatial planes in which the electric field is always zero, and other planes in which the magnetic field are always zero. There are even discrete times at which on spatial planes, both $\mathbf{E}$ and $\mathbf{B}$ are zero. Since these do not exist at all times, it becomes a bit difficult to discuss them 'moving', but a similar idea does appear.

In the original frame, away from a node the time averaged Poynting vector is zero, but the energy density is not zero. When transforming to the new frame, the components of the momentum and energy density will mix up (technically the stress energy tensor). So it should make conceptual sense that after the transformation the time averaged momentum density is no longer zero (also seen conceptually via your red/blue shifting argument).

So, does this count as a "standing wave"?
No. There are no longer constant node planes of $\mathbf{E}=0$ or $\mathbf{B}=0$, and there is now non-zero time averaged momentum density (so the stress energy tensor is that of something "moving" not "standing").

---

Calculation details:

Consider a standing wave formed from two plane waves travelling in the +/- x direction, linearly polarized in the z direction: $$\mathbf{E} = \mathbf{\hat{z}} E_0\left[\sin(kx - \omega t) + \sin(-kx - \omega t)\right] $$ $$\mathbf{B} = \mathbf{\hat{y}} B_0\left[-\sin(kx - \omega t) + \sin(-kx - \omega t)\right] $$

For a single plane wave, the nodes where $\mathbf{E}=\mathbf{B}=0$ are moving planes in space (so contiguous volumes in spacetime). For the above sum of waves, the nodes are still planes in space, but only show up at discrete times.

Looking at where the electric field is zero: $$\begin{align*} 0 &= \left[\sin(kx - \omega t) + \sin(-kx - \omega t)\right] \\ &= \sin(kx)\cos(\omega t) - \cos(kx)\sin(\omega t) - \sin(kx)\cos(\omega t) - \cos(kx)\sin(\omega t) \\ &= -2 \cos(kx)\sin(\omega t) \end{align*} $$ Similarly for the magnetic we will find: $$0 = -2 \sin(kx)\cos(\omega t)$$ which is similar, just shifted by a quarter wavelength in space and quarter period in time.

Focusing on the nodes in the electric field first, these are planes located at: $$ kx = \pi \left(n+\frac{1}{2}\right) \quad \rightarrow \quad x = a_n = \frac{\pi}{k}\left(n+\frac{1}{2}\right) $$ with $n$ any integer, for any value of $y,z,t$ (so a constant plane in space). The electric field will also be zero everywhere when $\omega t = \pi m$ with $m$ any integer.

For the magnetic field, there are planes located at: $$ kx = \pi n \quad \rightarrow \quad x = b_n = \frac{\pi n}{k} $$ with $n$ any integer, for any value of $y,z,t$ (again a constant plane in space). The magnetic field will also be zero everywhere when $\omega t = \pi (m+1/2)$ with $m$ any integer.

We therefore see spatial planes that show up with $\mathbf{E}=\mathbf{B}=0$ at $x=a_n,t=\pi (m+1/2)$ and at $x=b_n,t=\pi m$.

Let's define the new coordinates as a Lorentz transformation for the original coordinate system: $$\begin{align*} ct' &= \gamma(ct - \beta x) \\ x' &= \gamma(x - \beta ct) \\ y' &= y \\ z' &= z \end{align*}$$ with $\beta=\frac{v}{c},\gamma=[1-\beta^2]^{1/2}$.

The transformation laws written out for the fields gives the fields in this new frame as: $$\begin{align} & \mathbf {{E}_{\parallel}}' = \mathbf {{E}_{\parallel}}\\ & \mathbf {{B}_{\parallel}}' = \mathbf {{B}_{\parallel}}\\ & \mathbf {{E}_{\bot}}'= \gamma \left( \mathbf {E}_{\bot} + \mathbf{ v} \times \mathbf {B} \right) \\ & \mathbf {{B}_{\bot}}'= \gamma \left( \mathbf {B}_{\bot} -\frac{1}{c^2} \mathbf{ v} \times \mathbf {E} \right) \end{align}$$ While this is messy to write out in general, at the node planes all the components of $\mathbf{E}$ and $\mathbf{B}$ are zero, and so $\mathbf{B}'=0$ and $\mathbf{E}'=0$.

Note that since $v$ is perpendicular to $\mathbf{E}$ and $\mathbf{B}$, the previous spatial planes where $\mathbf{E}=0$ independent of time, or $\mathbf{B}=0$ independent of time, do not maintain this nice form after transformation as the electric and magnetic parts of the field will mix in the transformation. The only truly coordinate system independent 'nodes' are the ones in which the full electromagnetic tensor is zero.

Now all that is left is to find the coordinates of these nodes in the new frame. Here I'll just work it out for the $a_n$ planes.

In the original frame nodes are at spacetime coordinates $x=a_n$,$t=\pi (m+1/2)=T_m$ while $y,z$ can have any value. Therefore in the new frame $$ ct' = \gamma(cT_m - \beta x_n)$$ Simultaneity is broken, so instead of all spatial planes appears at the same time, they will occur in order down the x axis. If there was a series of bells on the x-axis that rang whenever the electromagnetic tensor was zero, they would ring simultaneously at a set period in the rest frame, but in the moving frame there would be like travelling waves of the bells going off along the x axis.

Since these are discrete events, as the transformation parameter $v$ is increased, there would eventually be aliasing effects, making it difficult to fully interpret as a moving "wave" of nodes.

$$ x' = \gamma x_n - \gamma \beta cT_m$$

So similar to the original frame, $y',z'$ can take any value (so the nodes are still planes), with $x'$ having discrete values (but now these values depend on time). With each appearance of a node $n$, it will move along the $x$ axis. As before, with larger $v$ aliasing of the discrete events makes it suspect to 'label' nodes by $n$ to watch them move along.

Some concluding remarks on the calculation:
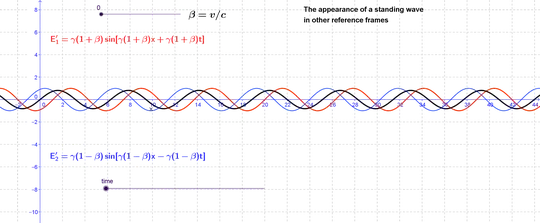
Since we started with a superposition of two plane waves, we could also write the result in the new frame as a superposition of two transformed plane waves. Since these waves will now have mismatched spatial and time frequencies, there will no longer be nice static planes of zero electric or magnetic field, but the nodes where $\mathbf{E}=\mathbf{B}=0$ still exist and allow us to mentally picture at least some features of the solutions.

Answer 2

The existence of the standing wave will depend on the reference frame of the observer.

One somewhat trivial way to look at this is to focus on the nodes of the standing wave in the rest frame. The way you have things set up, those nodes are nodes for the $E$ field; that means they are anti-nodes for the $B$ field. Applying the transforms to the moving frame, we get that $E' = -\gamma\beta B_0\hat{y}$, and $B' = \gamma B_0 \hat{z}$, where $B_0 = E_0/c$ is the magnitude of the $B$ field in the rest frame, and I'm taking your convention of the wave and $\beta$ moving along the $\hat{x}$ direction.

So what the observer in the rest frame sees as nodes of the $E$ wave, the moving observer doesn't see as nodes at all.

So what about the full wave? When I apply the transforms to the combined wave, I get the transformed waves as $$E' = E_0\gamma [(1-\beta)\sin(kx-\omega t) + (1+\beta)\sin(kx + \omega t)\hat{y}$$ $$B' = E_0\gamma/c [(1-\beta)\sin(kx-\omega t) + (1+\beta)\sin(kx + \omega t)\hat{z}$$ (NB: I was not very careful about transforming $k, x, \omega$ and $t$ when I did this. See the last section for why this is okay.)

The $\sin(kx - \omega t)$ terms represent waves traveling in the $+\hat{x}$ direction. Similarity, the $\sin(kx + \omega t)$ terms represent waves traveling in the $-\hat{x}$ direction. As $\beta$ increases, the part of the $E$ wave traveling with the moving frame gets weaker relative to the part traveling against the moving frame. The same is true for the $B$ field. In addition, both parts of both waves are scaled down relative to the wave in the rest frame.

A final note: Purcell actually talks about this in chapter 9. He comes up with $E_y' = E_0 \sqrt{\frac{1-\beta}{1+\beta}}$, $B'_z = E_0 \sqrt{\frac{1-\beta}{1+\beta}}$ for a single wave traveling in the direction as the moving frame. I believe that is equivalent to the result I have above, and the result you get in your answer (with an assumed $c=1$). If you reverse the direction of the moving frame, you flip the fractions in Purcell's result.

---

All observers will agree on the phase of this wave. The wavevector and frequency form a 4-vector $\mathbf{k} = (k_0, \vec{k}) = (\omega/c,\vec{k})$, while the position and time form the 4-vector $\mathbf{x} = (ct,\vec{x})$. Their scalar product must be a Lorentz scalar.

Here are two ways to this about this. First, qualitatively, from Jackson, 11.2A (page 519 in the 3rd Ed.):

The phase of a plane wave in an invariant quantity, the same in all coordinate frames. This is because the elapsed phase of a wave is proportional to the number of wave crests that have passed the observer. Since this is merely a counting operation, it must be independent of coordinate frame.

Second, by brute force. The scalar product $\phi = \mathbf{x}\cdot\mathbf{k} = \omega t - kx$ is the phase of the wave. In the moving system this becomes $\phi' = \mathbf{x'}\cdot\mathbf{k'} = \omega' t' - k'x'$. Plug in the Lorentz transformations (eq. 11.16 in Jackson) $x_0' = \gamma(x_0 - \beta x), x' = \gamma(x - \beta x_0)$ and the Doppler shift (eq. 11.29) $k_0' = \gamma(k_0 - \beta k), k' = \gamma(k - \beta k_0)$. Multiplying everything out gives you eight terms; four of them cancel out immediately, leaving you with $\phi' = \gamma^2(1 - \beta^2)(\omega t - kx)$. Recall the definitions $\beta = v/c, \gamma = (1 - \beta)^{-1/2}$, and the prefactors cancel, leaving you with $\phi' = \phi$.

Whichever route you use to convince yourself that the two observers will agree on the phase of a wave, that reasoning applies to both of the waves you have given in your thought experiment. So both observers will agree on the phase of $E_1$, and they will both agree on the phase of $E_2$. So whatever the overall wave looks like, they can at least agree on the phase.

Answer 3

This isn't a direct answer, but adds to Ben Crowell's answer and Curious Kev's answer and is simply something to help you have confidence in the correctness of your physical reasoning, which is perfectly sound.

Think of your standing waves in a box with perfect mirrors at either end, initially at rest relative to an observer $A$, and then you give the box a shove (instantaneous impulse) so that it begins to move at velocity $v$ relative to $A$. Now we look at the field, the instant after the shove, from the standpoint of an observer $B$ moving with the box.

As you correctly reason, observer $B$ classically sees the wave they are moving "with" at a lower intensity than the wave they are moving "against". Also, classically, they see the "with" wave red-shifted and the "against" wave blue shifted.

At the instant after the shove, before the mirrors have changed the light at all, the situation is exactly as you describe. The light moving with $B$ has a lower momentum than that moving against $B$. So the light has a nett momentum in the opposite direction to $B$'s motion relative to $A$. This nett momentum is the same whether you calculate it as (i) the same number of photons in either direction, but with the "with" photons red shifted and the "against" photons blue shifted or (ii) as you a have done, using the $E/c$ formula.

If the light is truly, losslessly confined inside the box, then a transient field variation results so that the frequencies of both "with" and "against" waves approach the geometric mean of the two frequencies and we again get a standing wave. The light's initial nett momentum is brought to nought. So, we conclude, the observer $B$ will see that there must be a time-varying force applied to the box to keep it stationary against the (dwindling) nett force exerted on the box by the imbalance of momentums.

So one physical meaning of your nett momentum in the moving frame calculation is this:

As the transients die out, the total impulse exerted by this force to stabilise the box's motion is equal to the nett momentum of the light in the box that $B$ calculated at $t=0$.

If $v<<c$, we find that the total impulse from either classical (like yours) or quantum (with photons) calculation is in fact $E\,v/c^2$. The confined light therefore behaves as having inertia $E/c^2$.

See a similar calculation, where I think about "squashing light" here.

Answer 4

Here is/was my attempt at a solution to this problem - thanks to the contributions of others here, I am now reasonably sure this is correct.

The setup is two plane, polarised waves travelling in opposite directions (let's say $x$). e.g.

$${\bf E} = E_0 \sin (kx + \omega t)\hat{\bf j} + E_0 \sin(kx - \omega t) \hat{\bf j}$$

The associated magnetic field will be $${\bf B} = -(E_0/c) \sin (kx +\omega t)\hat{\bf k} + (E_0/c) \sin(kx - \omega t) \hat{\bf k}$$

Now use the relevant transformations to derive the E- and B-fields in the frame of reference moving with velocity ${\bf v} = v\hat{\bf i}$.

$$ {\bf E^{\prime}} = {\bf E}_{\parallel} + \gamma [ {\bf E}_{\perp} + {\bf v} \times {\bf B} ] $$ $$ {\bf B^{\prime}} = {\bf B}_{\parallel} + \gamma [ {\bf B}_{\perp} - \frac{1}{c^2}{\bf v} \times {\bf E} ]\, , $$ where ${\bf E}_{\parallel} = {\bf B}_{\parallel} = 0$, $\beta = v/c$ and $\gamma = (1-\beta^2)^{-1/2}$.

At the same time, the wavevector and angular frequency are transformed according to the Lorentz transformations, but the wave travelling towards $-x$ is blueshifted, and the wave travelling towards $+x$ is redshifted.

The outcome of this is $$ {\bf E^{\prime}} = \gamma(1+\beta) E_0 \sin(\gamma (1+\beta)kx^{\prime} + \gamma (1+\beta)\omega t^{\prime})\hat{\bf j}\\ + \gamma(1-\beta) E_0 \sin( \gamma (1-\beta) k x^{\prime} - \gamma (1-\beta) \omega t^{\prime}) \hat{\bf j}\, , $$ and the B-field transforms in an analogous way.

So this is now the sum of two travelling waves with different amplitudes and frequencies. It is not a standing wave. As $\beta$ tends towards unity, the contribution from the second component essentially disappears and the resultant tends towards a pure, boosted version of the first component.

If you calculate the time-averaged Poynting vector: $$ < {\bf N} > = -\frac{2 \gamma^2 \beta E_0}{\mu_0 c} \hat{\bf i}$$

I have constructed a Geogebra applet that visualises this. I can only show snapshots here - the html5 applet is animated (though it's a bit clunky on my browser and you may want to download it, or click the show as java applet option at the bottom).

Below I show two snapshots. The first for an observer with $\beta=0$ i.e. the rest frame. The black line shows the resultant standing wave. Then an observer with $\beta=0.7$ sees the bottom picture (again, remember this is a snapshot in time). Notice how the resultant is now nearly coincident with the blueshifted (red) travelling wave.