11

Is there some historical reasons or is there a specific reason behind it?

This question is connected to: Why on-shell vs. off-shell matters?

Community
  • 1
Gunn
  • 113

2 Answers2

19

A particle is said to be on-shell if it satisfies the relativistic dispersion relation,

$$E^2 = p^2 +m^2$$

in units wherein $c=\hbar=1$. If you graph it, you obtain a hyperboloid surface (in 4-momentum space) for massive particles, and a cone for massless particles, like a photon. This is known as the mass shell, it is quite literally a shell or surface. The momentum of a real particle can be represented as a vector on the surface, hence the expression on shell. Virtual particles do not have these on the surface, hence they are off shell.

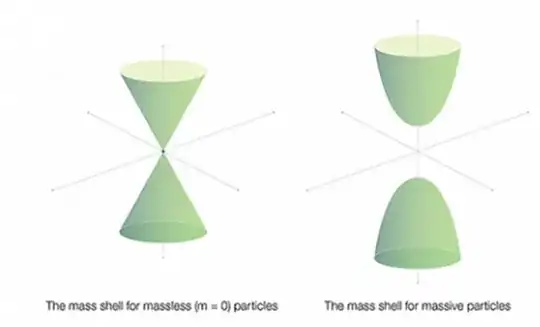
enter image description here

enter image description here

Source: Perimeter Institute, A Deeper Dive: On Shell and Off Shell

Constantine D.
  • 7
JamalS
  • 19,254
  • Of course, the term "on-shell" has broadened significantly to refer field or particle trajectories that obey the EoMs. – AfterShave Mar 30 '24 at 03:47
6

The term "shell" originally derives from the non-relativistic version of the answer by @JamalS. In a non-relativistic theory, a free particle satisfies the following dispersion relation $$ E = \frac{ {\bf p}^2 }{ 2m } $$ For a fixed energy a particle satisfies $$ {\bf p}_x^2 + {\bf p}_y^2 + {\bf p}_z^2 = 2 m E $$ In momentum space, this is precisely the equation of a spherical "shell" with radius $\sqrt{2mE}$. (See a plot here)

Now, in momentum space, the 3-momentum of a particle is described by a point. If $E$ is fixed, then the 3-momentum of the particle is only allowed to lie on the spherical shell described above, and is therefore said to be on-shell.

In quantum mechanics, a particle is allowed to not satisfy the dispersion relation. Thus, the momentum of a particle in quantum mechanics is allowed to not lie on the shell, and can be off-shell.

In a relativistic theory, the dispersion relation changes to $$ E^2 = {\bf p}^2 + m^2 \implies {\bf p}_x^2 + {\bf p}_y^2 + {\bf p}_z^2 = E^2 - m^2 $$ The corresponding constant $E$ surface is again a spherical shell, (this time of radius $\sqrt{ E^2 - m^2 }$)

Prahar
  • 25,924