For an object at rest is the potential energy completely zero?

Question

It is said every object in this universe tends to be at their lowest state of potential energy. What can be the lowest state of potential energy? And can the potential energy of an object be 0?

Answer 1

Potential energy as we measure it (not in general relativity) is only defined up to an additive constant. So indeed, we can always, and often do in Newtonian mechanics, take the potential energy to vanish at some point in the problem.

Think of how you would solve a "throw a ball up in the air" style problem. That is, consider throwing a ball up in the air with some constant velocity, and study it's motion.

Obviously it has gravitational potential when sitting on the surface of the earth. Explicitly this is given by

$$ V = -\frac{MG}{R_E} $$

where $R_E$ is the radius of the earth.

However this is irrelavant to the problem, so we subtract that value to take our earth-surface potential energy to be the zero potential energy point of the problem. Then we take the potential energy to be the difference between the surface of the earth, and the top of it's path:

$$ V = mgh$$

Furthermore, whether intentional or not, you were exactly correct when you said that "every object in this universe tends to be at their lowest state of potential energy". That is, they tend to be, but they do not necessarily have to be, nor are they always. There are such things as "unstable equilibria". These are configurations which have a local minimum of potential energy, but are not stable if they are disturbed.

Think of a bowling pin balanced upside-down for example. If it is balanced, and everyone leaves it alone, it will stay that way. However, if anyone disturbs it, even slightly, it will fall over. It will then try to find an even more stable equilibrium, the global minimum of the equilibrium.

Answer 2

Well, first of all potential energy is merely the difference in energy of a body due to the force fields it interacts with at any 2 points, this implies that there is no absolute standard to measure potential energy which in turn means there is no absolute 0 or any numerical value at all.

As far as achieving minimum potential energy is concerned, it is followed from the fact that forces act in the direction of reducing potential energy. If it is at all possible for a body to move to a position where it will have "comparitively" less potential energy then it will have forces that will guide it to that direction.

Since an absolute value is unrealistic, so is an absolute minimum. There is therefore no lowest value of potential energy. You can also see this fron the fact that gravitational potential energy is taken as negative, so if you go very close to a body your gravitational potential energy tends to negative infinity.

However any number you want to assign to the potential energy will only be relative to a previous number and not any absolute number. So although potential energy can be any real number, it would not mean much to anyone unless we know what system you are talking about and the past stages the body has been through!

Answer 3

For an object at rest is the potential energy completely zero?

The answer depends on the system considered; in our Hamiltonian if our potential $V$ does not depend on whether the particle is at rest, then the potential may be non-zero. In addition, the concept of a particle breaks down at scales close to the Compton wavelength, where we see 'swarms of particle-anti-particle pairs.' Hence, how can we even define a notion of a particle being at rest?

---

What can be the lowest state of potential energy?

The answer depends on the Hamiltonian considered. For a harmonic oscillator, quantum mechanically, the energies of each state indexed by a discrete parameter $n$, are

$$E_n=\hbar\omega\left( n+\frac{1}{2}\right)$$

The lowest possible state corresponds to $E_0=\hbar\omega/2$, which is above the minima of the potential. Of course, if we neglect quantum mechanical principles, then classically we take the lowest states to be precisely the minima of the potential in consideration.

---

Is it said that every object in the Universe tends to be at their lowest state of potential energy?

For most systems, they tend to be in their lowest energy state. However, there are exceptions. Consider a scalar field theory with a Lagrangian given by,

$$\mathcal{L}=\frac{1}{2}(\partial_\mu \phi)^2 - \frac{1}{2}m^2\phi^2 -\frac{\lambda}{2}(\phi^2-\eta^2)^2-\frac{\epsilon(\phi-\eta)}{2\eta}$$

The field theory has a true classical vacuum, corresponding to the state $\phi = \eta$, as the potential $V=0$. However, the state $\phi=-\eta$, is a classical false vacuum, providing $\epsilon$ is small relative to the height of the potential peak which divides both vacuums, c.f. the graph:

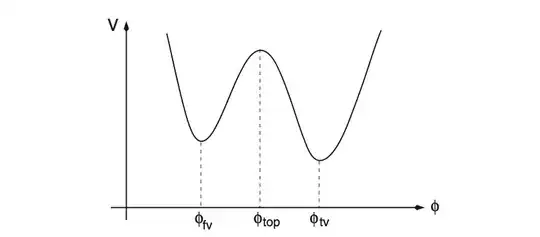
The false vacuum is metastable, and we would expect our system may be in such a state. However, a bubble nucleation process with true vacuum may occur, which expands converting false to true vacuum. Coleman and de Luccia deduce the implications and effects of gravitation on the process:

Vacuum decay proceeds by the materialization of a bubble. By energy conservation, this bubble always has energy zero, the sum of a negative volume term and a positive surface term. In the absence of gravity, we can always make a zero-energy bubble no matter how small $\epsilon$ is; we just have to make the bubble large enough, and the volume/surface ration will do the job. However, in the presence of gravity, the negative energy density inside the bubble distorts the geometry of space in such a way as to diminish the volume/surface ratio. Thus it is possible that, for sufficiently small $\epsilon$, no bubble, no matter how big, will have energy zero.

To re-iterate, it is conceivable for systems to occupy a metastable false vacuum. The work of Coleman and de Luccia has been extended, and many other gravitational instantons have since been constructed. A particularly interesting case is a false vacuum with inhomogeneities, such as a de Sitter black hole, which actually speed up the nucleation rate if one accounts for the conical singularities.

---

Image taken from Weinberg's Classical Solutions to Quantum Field Theory, page 255. For a link to the CDL paper, see link.aps.org/doi/10.1103/PhysRevD.21.3305 and for the paper by Gregory on black holes as bubble nucleation sites, see http://arxiv.org/abs/1401.0017.