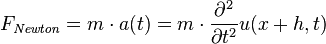When the two waves collide, why do they pass right through each other?
Mathematically it's due to the principle of superposition: the sum of the two solutions of a wave equation is also a solution. But intuitively it's not clear why the waves would not, say, just cancel each other during the collision.
What would be a convincing 'local' explanation - in terms of the individual particles in the medium (or segments of the medium), that move only due to the interactions with their neighbors?
Here's a simple example - two colliding wave pulses in the opposite phase with equal amplitudes and wavelengths (animation). In this case explanation is more straightforward (below). How would one make a similar argument for a general case?
In this special case the middle point acts as a fixed point, so that each wave pulse is 'reflected' from a hard boundary. In terms of individual segments: the one closest to the center is drawn to the equilibrium position by the force from the fixed point; it drags the next closest segment with it; etc. When they reach the equilibrium position they continue moving due to inertia and restart the wave in the opposite direction with the opposite phase. The reflected wave has the same amplitude and wavelength due to the symmetry around the equilibrium: the force on each segment at the opposite displacement is a mirror image of the original.
EDIT: elaborating on the question
Consider one of the particles on the spring-connected string, like in the bead-spring model (picture). It only interacts with its two neighboring particles - left and right. Now we send two wave packets moving towards each other along the string. For concreteness, let's say we are looking at the particle one to the right from the middle particle (the position where the two wave packets arrive simultaneously and first meet each other). First our particle is moved by its right neighbor due to the wave from the right reaching it. It moves like any other particle in the wave path. But then the particle on its left exerts the force on it, and that one has already been influenced by the wave from the left. Again, all the particle 'knows' is the position of its left and right neighbor. The question is: by just looking at its neighbors, how does our particle 'figure out' to have the displacement that is always equal to the sum of the two constituent wave functions at that point?