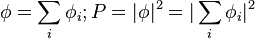QM probabilities do obey $\sigma$-additivity, however your sample space and probability measure change depending on what measurements you are making.
To use the classic example, consider a double slit experiment in which a particle can pass through two slits, $A$ and $B$, and hits a screen at point $x$. If we don't measure which slit the particle went through we can ask for, say, the probability that it hits the screen in the interval $[x_0,x_1]$ or the in the interval $[x_2,x_3]$ and we find that
\begin{align}
P(x_0\le x\le x_1) = \int_{x_0}^{x_1}\mathrm{d}x\,|\psi_A(x)+\psi_B(x)|^2
\end{align}
and similarly for $P(x_2\le x \le x_3)$. If the two intervals are disjoint it is clear that \begin{equation}
P(x_0 \le x\le x_1 \;\mathrm{or}\;x_2\le x \le x_3) = P(x_0\le x\le x_1) + P(x_2\le x \le x_3)
\end{equation}
so we have $\sigma$-additivity. However notice that our sample space is the space of possible $x$ values and makes no reference to which slit the particle went through. If we ask which slit the particle went through, we find that we no longer have a well defined probability, which is why we can't even sensibly talk about the question.
If we measure which slit the particle went through then we can ask for, say, the probability that it went through slit $A$ and hit the screen in the interval $[x_0,x_1]$. If we call the slit the particle went through $S$ we get an expression
\begin{equation} P(S = A,\, x_0 \le x \le x_1) = \int _{x_0}^{x_1}\mathrm{d}x\,|\psi_A(x)|^2\end{equation}
and we can come up with similar expressions for things like $P(S = B,\, x_0 \le x \le x_1)$ or $P(S = A,\, x_1 \le x \le x_2)$. If we now look at the probability for the particle hitting a point on the screen, regardless of which slit it went through, we do not get an interference pattern. i.e.\begin{align}
P(S = A\;\mathrm{or}\;B,\, x_1 \le x \le x_2) &= \int _{x_0}^{x_1} \mathrm{d}x\, |\psi_A(x)|^2 + |\psi_B(x)|^2\\
&= P(S = A,\, x_0 \le x \le x_1)+ P(S = B,\, x_0 \le x \le x_1)
\end{align}
so, again, we have $\sigma$-additivity, but we also have a different sample space, which now includes which slit the particle went through, and even if we some over this we have a different probability measure on the values of $x$.
In short quantum mechanical probabilities are always well-defined they are just not necessarily as well-behaved as you might classically expect, so we don't tend to think about them in those terms most of the time.