4

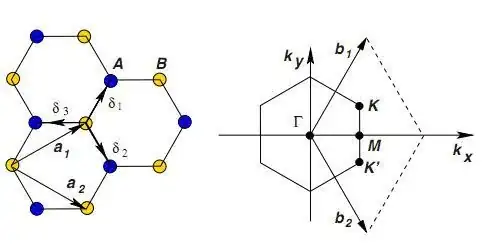
I've been reading about nanotubes lately, and I keep seeing the $ (n,m) $ notation. How does this describe a nanotube's structure? How do I determine which is $n$ and which is $m$ ?

I'm familiar with matrix notation referring to rows and columns, but I couldn't connect it with the nanotube structure which is, albeit predictable, not quite like a row-column grid.

Kit
  • 1,483

2 Answers2

6

In the picure below, you can see how the row-column grid correspond to the graphene structure.

Graphene structure

To have a (n,m) nanotube, you "just" have to roll your graphene sheet so that the (0,0) hexagon coincides with the (n,m) hexagon. Of course, it is much easier said than done !

Frédéric Grosshans
  • 10,943
  • édéric: Does "coincide" mean that the northwest edge of $ (0,0) $ will merge with the southeast edge of $ (4,3) $, so that it will form a seamless nanotube? – Kit Dec 03 '10 at 15:54
  • 1
    @Kit : No, the twot northwest edges will merge, as well as the two southwest edges. – Frédéric Grosshans Dec 03 '10 at 16:43
4

A carbon nanotube can be seen as a sheet of graphene that is "rolled up".

Now, graphene is a two-dimensional lattice and hence has two lattice vectors, $\vec{a}_1$ and $\vec{a}_2$. (If you are unfamiliar with lattice vectors let me know and I will expand on this).

The numbers $(n,m)$ simply state that your tube is obtained from taking one atom of the sheet and rolling it onto that atom that is at located $n \vec{a}_1 + m \vec{a}_2$ away from your original atom.

EDIT: Graphene is a tridiagonal lattice with two atoms per unit cell.

Left: Lattice structure of graphene, right: Brillouin zone (not of interest here)

Image source: The electronic properties of graphene. A.H. Castro Neto et al. Rev. Mod. Phys. 81, 109 (2009), arXiv:0709.1163, U. Manchester eprint.

Emilio Pisanty
  • 132,859
  • 33
  • 351
  • 666
Lagerbaer
  • 14,836
  • +1 The way I understand it, for an ordinary row-column grid, its lattice vectors are $90,^{\circ}$ apart. How does this generalize to a graphene lattice? – Kit Dec 03 '10 at 04:50
  • 1
    @Kit : You can have oblique coordinates in the plane. See http://mathworld.wolfram.com/ObliqueCoordinates.html – Frédéric Grosshans Dec 03 '10 at 13:59
  • 1
    I actually found the image you used in Figure 2 of Neto, et al. The electronic properties of graphene. 2009. I think it would be a courtesy to the authors to cite them, and also for me (and others) to help us know the relevant papers to read :) – Kit Feb 01 '11 at 12:47