Why does light bend towards the normal when passing from a rarer to a denser medium?

Question

Whenever light rays are entering a denser medium they bend towards the normal.

Why do rays choose the path towards the normal? Why cannot they choose the path away form the normal?

Answer 1

As mentioned here also remember that light has wave behaviour.

When a wave of water travels over shallow water, it slows down. This corresponds to light reaching a material of more "resistance" against its' wave motion (we simply measure that by measuring the speed of light in that material - the refractive index is the proporty $n=c/v$.)

This link shows a gif which is very illustrative: http://upload.wikimedia.org/wikipedia/commons/2/2d/Propagation_du_tsunami_en_profondeur_variable.gif

Now consider the same wave delaytion happening in 2D when a wave reaches the shore at an angle (as when the light is hitting the material at an angle).

The inner part of the wave, which hits the shallow water first, will start to slow down first. After that the rest of the wave follows gradually. This causes the gradual changing of the wave direction - the wave is slowed down and redirected because of this.

Whenever the light wave reaches a material of higher refractive index $n$, then the light waves will move slower in that material and this phenomenon will cause bending towards the normal. That is, towards the more direct route through the material. When light goes into a material of higher $n$ it speeds up and can therefor take a less direct route through the material in the same time.

Answer 2

See in Wikipedia the topic "Phase velocity" http://en.wikipedia.org/wiki/Phase_velocity and also Snellius law.

Let $M_1$ be a less refractive medium, and $M_2$ a more refractive one. Let $n_1$ respectively $n_2$ be their refraction indexes. It is known that in any medium the light wave has a phase velocity specific to that medium, and this velocity and the refraction index are interdependent.

Note, it's not the velocity of the light that changes from a medium to another medium. The velocity of light is c. It's the phase velocity that changes, and here below are some explanations.

The light propagation is described, in the simplest case, by $Asin(\vec k \vec r - 2\pi\nu t)$. The quantity $\phi = \vec k \vec r - 2\pi\nu t \ $ is called phase, and a surface on which at a given time $t$ the phase is constant, is called wave-front. The phase-velocity is the ratio of the distance between two neighbor wave-fronts of the same phase $\phi$, and the time $T$ needed for the light to travel a distance equal to the distance $d$ between two neighbor wave-fronts. This time is given by

$$ T = 1/\nu . \tag{i}$$

Note that the light frequency $\nu$ doesn't change from medium to medium, therefore $T$ doesn't change.

For illustration of the situation imagine the following scenario:

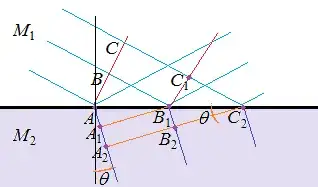
Consider a front wave of phase $\phi$ (red line) touching at the time $t_0$ the point $A$ on the separation surface between the two media, then at a time $t_1$ the point $B$ of the front wave touches a point $B_1$ of the separation surface, and at a time $t_2$ the point $C$ of the front wave touches the point $C_2$ of the separation surface. Let the points $A, B, C$ be chosen so as $t_1 = t_0 + T$, and $t_2 = t_1 + T$. As the velocity of the wave is smaller in $M_2$,

$$\frac {v_2}{v_1} = \frac {n_1}{n_2} \tag{ii}$$

the distance that the wave can travel during the time $T$ is smaller,

$$ d_1 = v_1 T, \ \ \ d_2 = v_2 T ==> d_2 < d_1 \tag{iii}$$

(hence the distance between two consecutive wave-fronts is smaller.)

In consequence, the angle $\theta$ of the wave-front with the separation surface is smaller in $M_2$ than in $M_1$. Finally, note that the angle between the front wave in $M_2$ and the separation surface is exactly equal to the refraction angle (i.e. between the normal to the separation surface and the normal to the wave-front).

Answer 3

i think it's because of least time principle that states "light tends to travel a path in least time possible." as simple as that