Why is $F=ma$? Is there a straightforward reason?

Question

Why is force = mass $\times$ acceleration? I have searched in many sites but didn't actually get at it. Simply I want to know that if a mass in space moves (gains velocity thus further accelerates), how can I think, postulate and further believe that force = multiplication of mass and its acceleration ?

Answer 1

I'm going to give you another approach.

Suppose that you were to perform the following experiments:

1.)

a) You happen to find a ball that is not moving. Well it's going to stay like that if we are in a place where the ball is not interacting with anything (air, gravity, etc.). Like this:

b) If you happen to find a ball that is moving with constant velocity, that is it moves in a straight line and it moves equal distances in equal times. Like this:

What we find is that if we are in a place where the ball is not interacting with anything (air, gravity, etc.). Something like this will happen Video of ball over ice. The ball will keep moving forever.

2.) Now suppose that the ball is not moving and you shot this arrow to move it, you have the same conditions as before:

As you can see the ball wasn't moving and now it is moving, so it accelerated. Suppose it has an acceleration $a_1$.

Now you look for a Weight scale and you find the mass of the ball:

You find that the mass is $m_1$.

Now you repeat the experiments with two balls of different masses, $m_1$ and $m_2$. That is you shot two arrows exactly the same.

As you can see the acceleration $a_2$ of the bigger mass is less that $a_1$ the one of the smaller one. If you multiply the two masses by its corresponding acceleration you find something 1 $S_1$ and something 2 $S_2$ , that is:

$$S_1=a_1\times m_1 \text{ and } S_2=a_2\times m_2$$

If you compare $S_1$ and $S_2$ you find that they are equal (BECAUSE OF EXPERIMENT !!):

$$S_1=S_2$$

This makes you think that the only thing that was the same in your experiment was the fact that you shot the arrows with the exact same conditions, so that thing that was the same is that we call force $F$. And we define that $$F=S_1=S_2$$

We say that the arrows hit the balls with a force $F$ and we find that useful because it is a quantity that let us predict what is going to happen, that is what is going to be the acceleration.

So from that we have experimental evidence that

$$F=m_1\times a_1=m_2 \times a_2$$

If we consider some arbitrary mass and force, we generalize to this with the known equation:

$$F=ma$$

Answer 2

Let's break this down in two pieces.

First - the proportionality of force with mass. Imagine you need a certain force $F$ to accelerate a mass $M$. Now imagine that instead of one mass, you have two - each with mass $\frac{M}{2}$. Attach a piece of string to each. The total force on the two strings must be the same as before, so each string sees half the force for half the mass. This should convince you that $F\propto M$.

Now for the acceleration part. Imagine the same mass as before, but now it is mounted on a train:

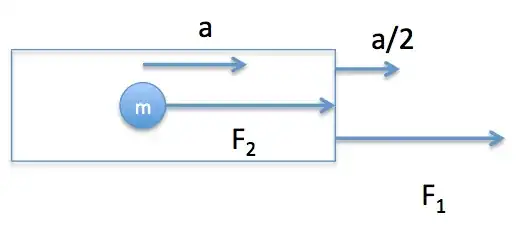
If the train is accelerating with acceleration $a/2$, you feel a certain force on the string holding the mass which is accelerating with $a/2$ - and the same force on the string pulling the train. If the train is standing still, you can "reel in" the mass, and still need the same force. But once again, you will need to apply that force also on the outside of the train in order to prevent it from moving.

Now if I try to accelerate the mass inside the accelerating train, I have to add these forces together. There is the force I need to move the train+mass with acceleration $a/2$, and the force I need to counter the force of accelerating the mass relative to the train.

From the above it follows that each of these is the same force - so when I double the acceleration, I double the force needed. It follows that force must be proportional to acceleration.

Putting these two together, you find

$$F \propto M\cdot a$$

The above only proves that $F$ is proportional to both mass $M$ and acceleration $a$ - the fact that it's actually $F=M\cdot a$ and not $F\propto M\cdot a$ is a matter of definition.

Answer 3

Force comes to play when the body is moving with changing velocity.

To quote one author's statement is rather noteworthy:

Force is the agent that is at the forefront for the initiation of the motion & also responsible for change in the velocity.

The famous relation can be deduced intuitively by means of calculus.

If $v$ is the velocity of a body of mass $m$ at an instant $t$, then its momentum at that instant is given by $$p = mv$$. The time rate change of momentum of the body at that instant is $$ \dfrac{dp}{dt} = \dfrac{dmv}{dt}$$. Acc. to Newton's second law, $$P \propto \dfrac{dp}{dt} \implies P = k. \dfrac{dp}{dt} = k. \dfrac{dmv}{dt}$$ where $k$ is the constant of proportionality. Since, mass $m$ of the body is constant(it need not be, it can change & this can be given as a function of time), we may write, $$P = k. m\dfrac{dv}{dt}$$. But $$\dfrac{dv}{dt} = \text{acceleration of the body} = f$$. Hence, $P = k. mf$. Now, if we agree that force that produces unit acceleration on unit mass will be called unit force ($P = 1$), then the equation yields: $$ 1 = k\cdot 1\cdot 1 \implies k = 1$$.

Addendum :

An interesting historical fact, often overlooked, is that Newton's own statement of the basic law of mechanics was not in the form of $P = mf$; it appears nowhere in Principia. Instead, Newton spoke of the change of "motion" by which he meant momentum & related this to the value of the product of force & its time of application. In other words, Newton's version of the second law was essentially $$P\cdot\Delta t = m\Delta v$$.

I would also like to jot down A.P. French's way to prove the law:

A.P. French's deduction of 2nd law:-

Let an object is placed on a horizontal table pierced with holes through which air is blown from below. It is then possible to pull horizontally on the object & make observations as the following:

1. A spring, stretched by a constant amount, causes the velocity of the object to change linearly with time - the acceleration produced in a given object by a given force is constant.

2. If a second spring, identical with the first & stretched by the same amount, is used side by side with the first, the acceleration is doubled. That is, if we take a known multiple of a force, then the acceleration produced in a given object is directly proportional to the total force.

It thus becomes possible to write down simple equations expressing the above relation: $$a = k.F \quad \text{or} \quad F = k' .a$$ where $k \quad , \quad k'$ describe the inertial properties of the particular object. Now, which result is more convenient??

Let's see:

If we place on the first object a second, identical object, it is observed that all accelerations produced by given arrangements of the sprins are reduced to half of what was obtained with one object alone. We can express this most easily by choosing the second equation, so that the inertial property is additive. $$F = (k'_1 + k'_2) . a_{1 + 2} \implies a_{1 + 2} = \dfrac{F}{k'_1 + k'_2}$$. It is by such steps that one can be led to the equation that is universally known as "Newton's (second) law": $$ F = ma = m\dfrac{dv}{dt}$$ where $m$ is the inertial mass of the object identical with $k'$ above.

Answer 4

If a particle is left alone in an inertial system, it will travel on a straight line, that is $$ \frac{d\vec{v}}{dt} = 0 \tag1 $$ it will not change the magnitude and direction of its velocity. This is an empirical fact. So if a particle does change its velocity the right hand side of (1) is not zero. Lets call it $\vec{A}$: $$ \frac{d\vec{v}}{dt} =: \vec{A} \tag2 $$. This is rather a definition for $\vec{A}$, because one can only measure the change in position and then assign a value for $\vec{A}$. Lets assume we know the cause of $\vec{A}$, e.g. because we applied the action of spring under tension to our particle. Furthermore we observed that $\vec{A} = \textrm{const.}$. If we now apply the same action to a second particle of double the mass what we will empirically observe is $$ \frac{d\vec{v} \ '}{dt} = \frac{1}{2} \vec{A} $$. This suggests that $\vec{A}$ is not an intrinsic property of the action (since we changed the particle and not the action) but rather $m\cdot\vec{A}$ is. One can now repeat that process with particles that don't differ in mass but for example in color, volume, etc. What one will find is that really only $\vec{A}$ and $m$ matter. Lets give that intrinsic property of action a name and call it force: $$ \vec{F} := m \cdot \vec{A} \ \underbrace{=}_{(2)} \ m \frac{d\vec{v}}{dt} = m \vec{a}$$ with $\vec{a}$ the acceleration of the particle. So the formulation of the equation of motion is the desire to find an expression with quantities that belong to delimitable subsystems only. In this sense $\vec{F}$ is an abstract quantity that is by definition equal to $m\vec{a}$.

Answer 5

The acceleration is the effect on the objects motion due to the cause(s), which is the vector sum/total of the forces acting on the object, i.e. the total force (composed of many forces) is responsible for the acceleration (which is just one vector). The mass is just the constant of proportionality that links total force and acceleration.

Answer 6

Simply put, it's a correlation between a certain action (applying force on a given mass) and reaction (gaining or losing velocity). The mass is a just a factor that was found to give accurate predictions in the world Newton lived in (relativity theory introduced a slight modification).

Both force (over time or distance) and velocity represent energy, that's why there's a direct relation between them.

This relation is held via the multiplication operator because of the type of proportionality between these qunatities, as observed in nature.

Answer 7

It's from the definition of mass, from this website, the definition of mass is

Mass, in physics, quantitative measure of inertia, a fundamental property of all matter. It is, in effect, the resistance that a body of matter offers to a change in its speed or position upon the application of a force. The greater the mass of a body, the smaller the change produced by an applied force.

and the definition of the unit of force, the Newton, from here

A newton is defined as the force which gives a mass of 1 kilogram an acceleration of 1 metre per second, per second

Once those terms have been defined the relation $F=ma$ follows from the definitions.