Double-double-slit with entangled photons

Question

Edited question to face complaints about ambiguity

Following experimental setup.

Bob uses a nonlinear crystal to create two entangled photons A and B.

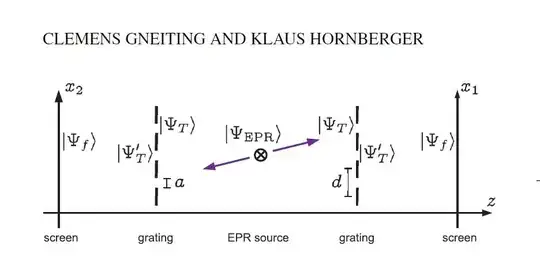
Consider a standard pair of EPR-entangled particles (correlated position and momentum values) with a joint wavefunction.

He sets up two double slits close to each other. I will refer to them as right and left double slit. (note that there are TWO double slits. Hence 4 slits total)

Photon A goes through the right double slit undisturbed.

Photon B runs through a long, coiled up, fiber optic cable, roughly 10 times the length of the distance to the moon, hence B will take about 10 seconds to come out at the other end. Bob decides to either disturb the photon by measuring some of it's quantum states or not to disturb it, depending on a coin flip he does at 8 seconds into the experiment.

(we ignore that we would require repeaters for lengths higher than 200km to keep it simple)

Instead of Bob creating just 1 entangled photon pair, he creates a million entangled pairs and goes on to check two cases.

case 1) Timeline: Bob creates 1 million photon pairs. Bob checks the pattern on the screen behind the right slit, the 1 million non-delayed photons (An) created. At about 8 seconds, Bob flips a coin. The coin turns out to be HEADS.

Bob allows photon B to go through the left double slit undisturbed after coming out of the fiber optics cable at around 10 seconds.

-

case 2) Timeline: Bob creates 1 million entangled photon pairs. Bob checks the pattern on the screen behind the right slit, the 1 million non-delayed photons (An) created. At about 8 seconds, Bob flips a coin which turns out to be TAILS.

Bob disturbs the photon B by doing some measurement(setting up a unit-efficiency quantum detector directly behind one of the two slits of the left double-slit) such that it would allow the "which path" to be known when going through the double slit.

The question is. Will the pattern the 1 million entangled photons (An) created on the right screen in case 1), be discernible from the pattern in case 2), in the sense of being able to state with high probability which of the 2 cases applies, by analyzing the distribution of the photons (An), which hit the screen after passing through the right slit?

edit: Or otherwise stated. Would we be able to make a statement, at 0-1 seconds into the experiment, by observing the pattern behind the right slit the non-delayed photons have caused, in the form of "the experiment has a higher/lower probability to take the course of case 1 rather than case 2", beforehand?

If the answer to that question is yes, then doesn't Bob already know (with high probability) at the beginning of his experiment (0-1 seconds), what the result of his coin flip at 8 seconds will turn out to be?

Before answering the question, i would like you to describe the pattern we would see (behind the right slit created by the non-delayed photons) in case 1) vs case 2), if we were to actually perform this experiment.

This is not the same as the delayed choice quantum eraser. We are using a million photon pairs, which is a different scenario, as the objection of many was that we cannot tell the interference/no-interference pattern by just observing a single photon. It's also different in the sense that we are just using two simple double slits, allowing us to not get lost in the details of different measuring devices.

edit: So i found a similar experiment proposed by John Hatter labeled "Superluminal information transmission using a double-double-slit apparatus"

In this experiment, the particles are entangled as follows: quote "Consider a standard pair of EPR-entangled particles (correlated position and momentum values) with a joint wavefunction"

He then uses a unit-efficiency quantum detector immediately behind A's left slit(B’s left slit in my case) to extract the which path information and therefore destroy the interference pattern.

quoting part of the document

Now, of course, left to themselves, both detection screens should exhibit the classic interference effect. Now however, take one of the double-slits (lets take A) and put a small, unit-efficiency quantum detector immediately behind A’s left slit. Let us be clear that the detector is directly behind A’s left slit and therefore well in front of the screen. In fact, let the detector be so close to the slit that if we ever get a hit, we can say with a high degree of certainty which path the particle took. This should (of course) destroy the interference pattern on the detection screen behind double-slit A since we now have whichpath information for A. But consider our results derived above ... since the scattering potentials of A & B double-slits are conjugates, when the particles encounter their respective double-slits, their paths will be correlated . In other words if one particle uses the left-slit path of A, the other must use the left-slit path of B...

(in my experimental setup B is the equivalent of A in the setup John Hatter proposed)

Conclusion: It does not take much work to see how this could be used to perform superluminal signalling. By allowing EPR-entangled particles to propagate in an environment similar to that described above, and by sequentially destroying and preserving the interference effect, information could be transmitted. Since the interference effect is destroyed as soon as we gain knowledge of which-path

I hope that satisfies some as in defining the experimental setup more precisely.

Answer 1

Your question is muddled and unclear (in my professional opinion - you may think otherwise and that's OK), but I think I can make one thing clearer.

• If you have two entangled systems, $A$ and $B$, and perform independent experiments on either side, then nothing about the choice of experiment you perform on $B$ will have any effect on the local results from $A$.

Note the keywords independent and local. If you look for correlations between the two experiments, then the situation can change. Thus, if you post-select the results from $A$ to include only the runs when $B$ performed experiment $B_1$ and obtained outcome $B_1(+)$, then the post-selected results from $A$ will depend, in general, on both the measurement and the outcome.

---

Having said this, I will continue to hammer on on what's been said before: your question is essentially undecidable unless you specify exactly what type of entanglement you imagine both photons to share. You seem to have a magical view of entanglement (which is alarmingly common) in which touching system $B$ will immediately and irrevocably change everything about system $A$, which is very, very far from the truth.

Allow me to elaborate by presenting two scenarios, which I believe are consistent with how you phrased your question:

Scenario 1

The photons are entangled in polarization, sharing the state $|HH\rangle+|VV\rangle$, but are otherwise indistinguishable.

In this case, nothing you do on $B$ will have any effect on the interference pattern (or lack thereof) shown in $A$, because the entanglement simply does not couple to the spatial modes.

Scenario 2

The photons are spatially entangled, in such a way that when photon $A$ hits its left slit then photon $B$ hits its right slit, and vice versa, i.e. they share the state $|LR\rangle+|RL\rangle$.

In this case, your actions on $B$, both your choice of measurement and the corresponding experimental outcome, can affect the results of $A$ if you postselect on the appropriate results on $B$, at least in principle. Other choices of measurement in $B$ will not have any effect on $A$. In particular:

1. If you perform a path measurement on $B$, where you detect which-way information for it, then (in this scenario) you also make available which-way information on $A$, which precludes it from showing an interference pattern. This is independent of the temporal sequence and spacing between the two measurements, and on whether the measurement in $B$ was randomized or not.

2. Suppose, on the other hand, that you do nothing with the photon in $B$ and allow it to run through the slits undisturbed. In this case (for this scenario), you will not observe any interference pattern on either photon. The reason for this is that each photon contains (in principle) which-way information on the other, so that the other one cannot interfere. The reduced state for both is $$\rho=\frac12\left(|L\rangle\langle L|+|R\rangle\langle R|\right),$$ and no coherent dynamics can be extracted from it. This is independent of the temporal sequence and spacing between the two measurements, and on whether the measurement in $B$ was randomized or not.

3. On the other hand, within this scenario there is indeed one measurement choice on $B$ which can restore the interference pattern on $A$, and it is of course the quantum eraser scheme. If you measure in the basis $\{|+\rangle,|-\rangle\}=\{|L\rangle+|R\rangle,|L\rangle-|R\rangle\}$, then the detector on $A$ will not turn up any interference pattern, but if you post-select and separate the counts on $A$ which coincided with $|+\rangle$ and $|-\rangle$ detections on $B$, then the blob will separate into two complementary interference patterns.

   This behaviour is independent of the temporal sequence between the two measurements, their temporal separation, and whether the measurement in $B$ was randomized or not. If the measurement in $A$ is performed before the randomized decision to measure in $B$, then you have the delayed-choice quantum eraser experiment, which has been analyzed in detail elsewhere and which I will not attempt to clarify.

   Note also that in the latter case, there is no measurement at $A$ that will enable you to predict the outcome in $B$. This is, again, exactly the same as with the delayed-choice quantum eraser, regardless of however many photons you send.

---

These two scenarios demonstrate that your question is ill-defined - the precise answer depends on information not contained in the question.

---

Some additional notes:

• The measurement outcome is independent of however many photons you send through. Even in case 3 of scenario 2, if you try to send a million photons and observe the screen before you measure (or decide the measurement basis, or toss your coin, or whatever) on $B$, what you'll see in the screen in $A$ is... nothing, just an interferenceless blob. This is because each photon is an independent run of the experiment, and will have an independent result on the $|\pm\rangle$ basis, so if you add them up you are already performing a decision of what you'll do with the results from $B$.

• The need for many photons to detect an interference pattern is a red herring; the "objection of many" is only raised by people with a hazy understanding of the quantum eraser experiment.

  The goal is to detect coherence between $|L\rangle$ and $|R\rangle$ on the $A$ side, and this can be done without the need for a large number of photons, by being more clever about it. More specifically, you should collect the light behind each slit with an optical fiber and then shine them onto a beam splitter with detectors $M$ and $N$ on the output ports, calibrated so that $|L\rangle+|R\rangle$ will go exclusively into $M$ and $|L\rangle-|R\rangle$ will go exclusively into $N$. Thus a single count in $M$ rules out $|-\rangle$ and a single count in $N$ rules out $|+\rangle$.

  This scheme is (provably) optimal. It will, of course, not give you enough information to completely determine the state from a single run of the experiment; this, however, is a fundamental limitation and the only way to get around it is via quantum state tomography.

• This answer represents my best attempt in good faith to make sense of your question, which is a very tall proposition. If you feel I have not understood any aspect of the question, I would encourage you to think long and hard about how you are phrasing your post, instead of chucking more rep at it. Science depends crucially on its communication, and this includes making sure that one's audience can understand the material. If the entire audience says it is too obscure, blaming the audience will not benefit you at all; instead, try to clarify the material, and politely ask your audience what else you could do to make the point more evident. (If you want to, of course. Blaming the audience is lots of fun too.)

Answer 2

Will the pattern the 1 million entangled photons (An) created on the right screen in case 1), be discernible from the pattern in case 2), in the sense of being able to state with high probability which of the 2 cases applies, by analyzing the distribution of the photons (An), which hit the screen after passing through the right slit?

No, the pattern of the million photons (An) will be the same in both cases.

Would we be able to make a statement, at 1 seconds into the experiment, by observing the pattern behind the right slit the non-delayed photons have caused, in the form of "the experiment has a higher/lower probability to take the course of case 1 rather than case 2", beforehand?

No, the pattern of the million photons (An) will be the same in both cases.

Can you describe the pattern we would see (behind the right slit created by the non-delayed photons) in case 1) vs case 2), if we were to actually perform this experiment.

The exact pattern will depend on the angle of the screen to the slits and the incoming wave as well as the distances. It will be the same in case 1 and in case 2. As others have mentioned there are multiple ways to entangle photons because they have polarization degrees of freedom as well as spatial degrees of freedom, and you haven't said which degrees of freedom you entangled. but if you had polarization degrees of freedom (say from Spontaneous Parametric Down Conversion) then you can pass it through a crystal that sends different polarization states on different trajectories and aim each trajectory towards a different slit and space the slits far enough apart relative to the beam width to turn polarization entanglement into spatial entanglement.

So I'll assume you've done that.

This means the pattern on the right screen (the double slit that gets used first) looks exactly like that you'd get if you had setup which-way information, i.e. take the frequency histogram for each single slit and add the frequencies together to get the total frequency. So two big peaks that drop down less in between them than how quickly the drop off farther from the center region.

The only way to see an interference pattern would be if you groups all the million hits (that have already happened) into different groups each group making waves that complement each other (peak near trough and vice versa).

The easiest way to see this for yourself is to note that measuring the B photons is a way to measure the which way information, so when you look at the results from (An) you are indeed looking at the results of a which way double slit experiment, so that is what the results look like. The interference pattern is lost in situations where you could find out the which way information, not just when you actually bother to find it.

And it happens for actual mathematical reasons, nothing to do with human intentions. You can imagine that hitting the screen with which way information is just like hitting a different screen or a different part of the screen. They just don't get the opportunity to interfere unless they have the chance to hit the screen in identical enough ways. The degrees of freedom that are given to the other particles makes it so they can't hit the screen in identical ways. Only identical outcomes can interfere.

This is not the same as the delayed choice quantum eraser.

It's hard to see any difference, you just happen to have such a high density of particles coming in at such a rate that a million photons hit the first screen before the second delayed part is set up fully. It think it merely changes how you talk about it and thus how people talk to you about it. It doesn't change the physics. The physics is still about the results at the two screens and about the potential correlations between the results on the two screens (which itself is about breaking the collection of all hits on the screen into two subgroups). The potential division into the two subgroups doesn't happen until you start to get results from both halves of the entangled pairs. It is not related to how many hit the first screen before you set up the second screen. In this new question it happens that you don't start to get results from the second screen until after all the hits on the right screen (An) are done. But that changes nothing at all.

It's also different in the sense that we are just using two simple double slits, allowing us to not get lost in the details of different measuring devices.

It's not just the measuring devices, those half-silvered mirrors in the delayed choice quantum eraser were putting phase differences on the parts that were reflected versus the parts that were transmitted.

Answer 3

I could give a shorter then the other answers because of a different understanding how a double slit works. See my questions and answers in this forum.

Every photon with its E and B field components get into interaction with the surface electrons from the slits material. Their field is quantized and this we see as fringes. Diffraction we not only get behind double slit, but behind every edge, and this for single photons too.

Knowing this, it is easy to give a short answer. The result of your experiment depends from the result of your method of entanglement. For example, if entanglement leads to polarized photons one could see fringes behind edges if the polarised photons hit the edges under more then 45° to the edges position or not. Simple you have a polarization filter. To the photons you've send to the moon happens nothing different. Only you disturb them or you not and get fringes or not.

I have a different view on entanglement too. Using a spezial crystal you generate the entangled photons with two definden states. That we could know which state belongs to which photon does not mean that the states are not defined at the moment of their production. The collapse of the wave function and the wave function be itself are mathematical expressions. The collapse means that our not-knowledge about the states collapses. Nothing about spooky Fernwirkung.

So don't losee your time with phenomena which where wrong interpreted since hundred years because of not having the knowledge we have today.

Answer 4

I will answer your question, in short.

A single beam of entangled photons will not create interference pattern. In fact entanglement of photon, before or after passing through the double slit, will extract which-path information and therefore will not produce interference pattern. It is correct, regardless of what you will do with the other entangled photon which has not passed through the double slit (at any time in any location).

Answer 5

I faced the same question and I write an article on this subject.

Let’s consider a beam through a device that produces entangled photons like BBO or similar crystal travelling in the opposite direction like in FIG.1

The 4 slits experiment consists of two double slits in opposite side connected by beams that are entangled each other. What happens on the screens? Let us consider the screen on the side D2. If you measure something on this side, i.e. if you look at the hole the photon passes through, the measure will destroy the interference on the screen. We usually say that the measure collapses the photon and its nature changes from wavy to corpuscular: the interference in D2 side disappears.

And in the opposite side in D1?????? In D1 in FIG2 by one hand we don’t know from which slit the photon passes through (indistinguishability of the paths) and so we expect interference. On the other hand if it is entangled with the first photon the behavior should be the same like the first one and so collapse without any interference. The question could be reformulated in the following way: are the two photons entangled in position tied between them up to the point that the collapse of one makes immediately the collapse of the other? Is duality a property that spreads at mascroscopic distance (distance greater than that allowed from light speed) between twin particles? You can expect that to destroy the interference on the D2 screen reflects the same behavior on the screen D1, i.e. that entanglement prevails over the not knowledge of which way passes on D1 side. This gives the advantage to operate on the side D2 without touching the side D1; therefore we can imagine a second part of experiment with “delayed choice” as follows: The 4 slits experiment has a natural prosecution, almost obvious, simpler than other similar (because the beam is split before it impinges on the slits). Trap the photon on one side between mirrors and leave the other photon towards the double slit. There we should observe the interference. At this point, after the interference has occurred, leave the other photon from mirrors and leave it to go towards the other double slit and reveal it. Destroy the interference on the other side at later time … What can happen? Can the interference already occurred be back? It seems a quite simple experiment. You can imagine that someone has done it and so after a long search in Internet this article pops up 1: Nonlocal Young tests with Einstein-Podolsky-Rosen-correlated particle pairs The system of the experiment, in FIG.3, is essentially the same but more general.

The experimental equipment is the one in FIG3. They consider the double slits or gratings on both sides. The gratings are the equivalent of the double slits but they improve the visibility of the fringes of interference. They consider also the possibility of non symmetrical gratings (step a in one side and step d in the other) and talk in general of a pair of particles and not only of photons. Happy to have found an analogue experiment and at the same time completely astonished. The author said “Even for a source emitting ideal EPR particle pair no interference will be observed at each of the detectors”. They talk about a non-local interference revealed considering synchronicity of time at both screens x1 and x2. So reporting the result at our configuration we’ll have the next FIG4 FIG.4 No interference in D1 nor in D2? It seems an experimental set but I really found other theoretical scholars that have conceived the same experiment and resolved it analytically using modular variables. Will it be true? Duality of Englert and Greenberger Many theoretical physicists (Englert [2,3,4], Wootters and Zurek [5], Greenberger and Yasin [6]) that have studied the double slits have proposed a generalization of complementarity, represented by the inequality V^2 + D^2 ≤ 1 It becomes equality for pure states V^2 + D^2 = 1 (1) where V is the visibility of the fringes and D is the distinguishability of the path. FIG.5 Standard schematization of Young’s experiment. We can write the state of the photon after the double slits as |> = |> ⊗|>+ |> ⊗|> With ca e cb arbitrary coefficient normalized in the way that | ca |2 +|cb|2 = 1. In that expression |A> e |B> are states of the single photon passing through the slit a or b and no other photon anywhere and |> |> are normalized states of any other degre of freedom of the photon (polarization, temporal mode, ecc) with arbitrary correlation stated by <|> =| | 0≤| |≤1. The quantification of the particle or wavy aspects are visibility and distinguishability defined as follows V=2 | |cacb/ca^2+cb^2 where ca^2 e cb^2 are measures of probability that photon passes through slit a or b respectively and | | is the correlation coefficent. The visibility is also called Contrast in Greenberger and Yasin [13]. Being ca^2 = Ia e cb^2 = Ib we can also write [9, 13] = I− I / I+ I =2||√+ Where Ia e Ib are measures of probability that photon respectively passes from a or b For distinguishability =|−+| If the indisturbed light impacts on the double slit, Ia = Ib are equal probabilities that the photon passes through a or b, i,e, indistinguishablity of the path, and V = || D = 0 Maximum visibility of the fringes and no information about which way. Instead if we know the path through the photon passes, then Ia = 1 e Ib = 0 (or viceversa), and V = 0 D = 1 No interference, i.e zero visibility of the fringes and maximun distinguishablity, that is certainty of the path. With this notation the concurrence C [7], that represents a measure of the degree of entanglement, becomes C = 2√(1−||2) We note that concurrence is zero when ||=1 and for that value of visibility reaches its absolute maximun V=1. We’ll tell about it afterwards. V^2 e D^2 are both within the range from 0 to 1. Duality reappears in the double slits. The quantum system represented by the double slits can exhibit wavy (V≠0) or corpuscular (D≠0) behavior, but heavy presence of wavy behavior reduces the corpuscular one and viceversa. This concept is quantitatively expressed by eq. (1) where V, the visibility, represents the fraction of wavy behavior and D, the distinguishability of the path, represents the fraction of corpuscular behavior. The classical complementarity wavy corpuscolar is expressed by one of the two limit conditions, that are mutually exclusive: the point (1,0), V=1 and D=0 doesn’t tell any information on which way and full visibility of fringes of interference. Otherwise the point (1,0), V=0 and D=1represents full information on the path and no interference. However intermediate values are available, for ex. V^2=06 e D^2=04 (all points in the quarter of circumference on the first quadrant). These possibilities are typically quantum conditions that can’t be brought back at the classical dualism (x ray and proton in everyday language let us think to rx as electromagnetic waves and protons as particles, but they are similar, both of them have some of one and other). To leave indefined the quantistic nature of quantum objects we don’t talk anymore of waves or particles, we can use the word quanton proposed by M. Bounge in 1967 [8]. Quanton is a new word to substitute the couple wave/particle. The control of duality The duality between fringes and which way information has been recently extended by Rochester University articles [9, 10, 11] introducing another term C, called concurrence, that measures the percent of entanglement, and eq, (1) becomes

V^2 + D^2 + C^2 =1 (2)

Where V is the visibility of fringes, D the knowledge of path and C the measure of entanglement. This new equation adds the concept that the entanglement forces more or less duality, to the limit of zero duality for complete entanglement, i.e. C=1. With this equation we can gain insights for the initial situation of the 4 slits: C=1 complete entanglement (for construction), D=0 we don’t know which way. With these two values we are obliged to conclude V=0, i.e. no fringes of interference! Not even at the beginning. What is this light that doesn’t make interference at the grating? Entangled photons are different from free photons. As though they were not delocalized. Entanglement identifies them as a couple, and they are not anonymous anymore in the multitude but localized … as a couple. The entanglement is an intrinsic characteristic, like an inner dimension of light. Entanglement known for coupling particles in instantly and non-local manner had the effect to bring photon onto corpuscular side too. One intrinsic connection between concurrence and polarization is shown in [9, 12]

P^2 = 1 − C^2 (4)

Where P is the degree of polarization with 1 ≥ P ≥ 0 and C concurrence, with C between 0 ≥ C ≥ 1. Polarization and concurrence are perfect antagonists in Young double slit [13,14]. We found once again the duality between concurrence and polarization as if the light could swing internally between wavy and corpuscular personality. When P^2=1 light is completely polarized and it is a wave in Young interference. Instead with concurrence C^2=1 is completely non polarized, from (4) P^2=0, and it is at the top of his corpuscular nature. The 4 slits experiment should be easy to realize with the today technology. In this test entangled undisturbed light beam doesn’t make interference at Young‘s double slits. Is a context where should be possible to observe directly the corpuscular nature of light. This article formatted with abstract and reference here https://www.academia.edu/66730927/The_4_slits_experiment

The conclusion is the same no interference in any of the screen. Entanglement switches off the wawy personality of the light