In my AP physics guide the graph for electric potential (for a radial field, i.e. point charge) and gravitational potential (for radial field, i.e. point mass) slightly differ from each other and I want to know the "math" behind this.
The one given for gravitational potential:

Ones for electric potential:
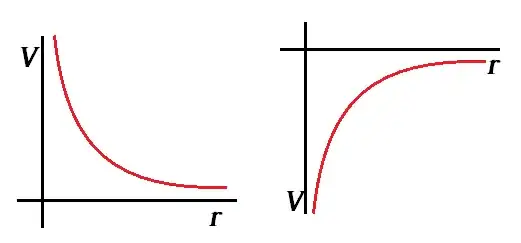
I am not worried about there being two graphs for electric potential because I know this is because electric potential is positive or negative depending on the charge whose electric field is being described. However, I noticed that the gravitational field graph only starts at $R_E$, which is defined in the book as being the radius of the mass we are describing. On the other hand, there is no corresponding $R_E$ for the electric potential graphs. Does that mean that electric potential is also defined inside a charge as well as above its surface? (I assume gravitational potential is not defined inside a mass because the given graph for gravitational potential stops at $R_E$)