11

Everyone who has been interested in modern science has heard explanations (certainly simplifications) of general relativity, mostly that space is curved. The analogy with a rubber sheet is popular. In such an analogy, orbiting planets are said to be naturally following "a straight line in a curved space".

Assuming that is not an oversimplification, would it mean that orbits are loops generated in space by massive objects ?

Also, if we consider spacetime as a curved structure, thus lines are not necessarily straight, what would be the meaning of momentum in such a frame?

Jim
  • 24,458
Golz
  • 189
  • I'm not sure of the motivation behind this question: aren't orbits "loops" in Newtonian gravity too; and don't curved paths have a momentum at every point even in flat space? – AV23 May 19 '15 at 17:11
  • What confuses me is that a "curved path" in a curved space is really a straight path (assuming the curvature of the path is the same that the one of said space) – Golz May 19 '15 at 17:14
  • "Cylinder" is probably a better description than "loop" for what people think of by the word "orbit". It's the cross sections of the cylinder (e.g. what you'd 'see' in an 'instant of time') that are loops. –  May 19 '15 at 19:26
  • You're ignoring the "time" part. And in fact, quite a bit of the "space" part as well. Don't forget that GR is local - it works the same whether you look at a volume in orbit around Earth, or the whole solar system. While it might make some measure of sense to talk about a "loop" relative to the Earth, it doesn't make sense for anything smaller or bigger. In fact, looking at it like this, Newtonian gravity is a lot more "loopy" than GR. – Luaan May 20 '15 at 08:43

4 Answers4

23

Calling orbits loops is a dangerous line of thinking. Objects that are not under the influence of other forces follow geodesics, which are the curved space equivalent of straight lines. And, while it's tempting to say that the orbit of a planet is effectively a loop in spacetime, let me try to convince you why such a simplification should be avoided.

Yes, for the orbiting planet, it follows a geodesic through spacetime that ends up leading it around the host star in a loop. So for the planet, you could say that the star's mass has warped spacetime such that a straight line is now a loop. However, consider objects with other velocities. For instance, consider a beam of light. Light follows a straight line through space as well. But if you shone a beam of light tangent to the planet's orbit, it would likely not loop around the star. So how can we say that the star's mass has generated a true loop in space if not everything follows this loop? We can't. Spacetime is most assuredly curved, but every observer sees their own curvature. It isn't so simple that we could say a star curves a straight line into a loop when not everything would move around it in a loop. The relationship between gravity, velocity, and curvature is a complicated one and oversimplifying by saying that gravity makes straight paths into loops in space is liable to do more harm than good.

As for the meaning of momentum, that does not change. $\sqrt{\frac{E^2}{c^2}-m^2c^2}$ is still the definition of momentum and it still refers to the energy stored in an object's motion through spacetime.

Jim
  • 24,458
  • One should not, that light follows different geodesics than massive particles (as they follow null geodesics with the property $u^\mu u_\mu = 0$), while the geodesics for particles have the property $u^\mu u_\mu = 1$. – Sebastian Riese May 19 '15 at 17:32
  • @SebastianRiese naturally. I believe that the fact that there are different geodesics at all was the basis for why I was saying one shouldn't say orbits are loops. – Jim May 19 '15 at 17:34
  • Even an orbiting planet doesn't go around in a loop, as GR causes precession of the perihelion. – user1247 May 19 '15 at 19:31
  • @user1247 If the orbit is perfectly circular, the perihelion can precess all it wants and the orbit would still be a loop. And I'd still say it shouldn't be called a loop anyway – Jim May 19 '15 at 19:49
  • Fine, but the set of orbits that are perfectly circular are measure zero. – user1247 May 19 '15 at 21:43
  • 4
    Isn't it still not a loop, unless the planet ends up at the same time one orbit later (as well as the same point in space)? – user253751 May 20 '15 at 05:26
  • @immibis that's a loop in spacetime. The OP suggests a loop in space only. That said, I won't argue with anyone coming up with additional reasons not to call this a loop. – Jim May 20 '15 at 13:52
17

No.

A loop has to start and end at the same point. In GR that means it has to start and end at the same spacetime point i.e. the same point in time as well as the same point in space. Such loops are called closed timelike curves, and with the exception of some obviously non-physical geometries they do not exist.

John Rennie
  • 355,118
  • 1
    So it is not a loop in spacetime, but is it a loop in space ? – Golz May 19 '15 at 17:16
  • 2
    @Golz: in GR you cannot make a unique split between time and space. You might say that a planet has returned to the same point in space (at a different time) therefore it has moved in a loop. However other observers would disagree. Even the simple case of an observer moving relative to you would claim the planet moves in a helix not a loop. – John Rennie May 19 '15 at 17:18
  • Thank you for you answer, I've also found a thread that treats the same question here link – Golz May 19 '15 at 17:26
  • If something starts and ends at the same point in spacetime, did anything really happen? – Michael McGriff May 19 '15 at 18:56
  • I guess it would be more of a helix in the time dimension. – Sam Washburn May 20 '15 at 05:17
6

Everyone who has been interested in modern science has heard explanations (certainly simplifications) of general relativity, mostly that space is curved.

I'm afraid that those explanations that say space is curved are misleading. See Baez: "Similarly, in general relativity gravity is not really a 'force', but just a manifestation of the curvature of spacetime. Note: not the curvature of space, but of spacetime. The distinction is crucial". Curved spacetime is a "curved metric", and a metric is to do with measurement. For example, you place optical clocks throughout an equatorial slice through the Earth and the surrounding space, then plot the clock rates. You depict lower slower clocks as lower down in a 3D image, and higher faster clock rates higher up. What your plot looks like, is this:

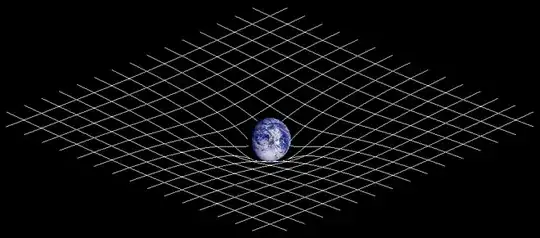enter image description here CCASA image by Johnstone, see Wikipedia

That's a picture from the Wikipedia Riemann curvature tensor article. It's a depiction of curved spacetime. And because it's derived from optical clock rates, it's a plot of the "coordinate" speed of light. Your plot of measurements is curved, space isn't. Instead space is inhomogeneous, and because of this light curves and matter falls down. Note that you need the curvature to get the plot off the flat and level - you need the curvature to get the slant, but the curvature relates to tidal force while the slant relates to the force of gravity.

The analogy with a rubber sheet is popular. In such an analogy, orbiting planets are said to be naturally following "a straight line in a curved space".

The rubber-sheet analogy isn't quite right, but it isn't totally wrong either. The planets move a bit like marbles on a rubber sheet. The slant makes them veer towards the Sun, so they end up going round and round.

Assuming that is not an oversimplification, would it mean that orbits are loops generated in space by massive objects?

No. Orbits are the curved paths of objects moving through inhomogeneous space and so subject to the force of gravity. The central massive object "conditions" the surrounding space, altering its properties, the effect diminishing with distance.

Also, if we consider spacetime as a curved structure, thus lines are not necessarily straight, what would be the meaning of momentum in such a frame?

I'm not sure what to say. Spacetime can be thought of as a "block universe" that models motion through space over time as geodesic worldlines. Worldlines don't move, and objects don't move up them. To get the gist of this, use an old-style movie camera to film a red ball flying across a room. Then develop the film and cut it up into individual frames, then form them into a block. There's a red streak through the block. That's like a worldline. But there's nothing moving in or through the block, nothing at all. Momentum would be where the streak wasn't vertical because the ball was moving. A curved streak would represent acceleration or changing momentum.

John Duffield
  • 11,097
0

"Straight lines" in curved space are geodesics. But the geodesics that define particle paths are in the pseudo-Riemannian manifold of space-time, they are not geodesics in space!

As a planets path is not closed in space-time (but some kind of spiral), massive bodies do not induce loops in the topology of the space-time. (Actually the loop is not even closed in space, due to the perihelion shift).

The momentum is defined in terms of the energy-stress tensor, which fulfils the conservation law $$T^{\mu\nu}_{;\nu} = 0.$$ As this reduces to the classical momentum and energy conservation locally upon taking the limit that leads to Newtonian mechanics.

Furthermore, if the space has a Killing vector field $\xi^\mu$ (that is a continuous symmetry), the quantity $\xi^\mu x_\mu$ is conserved along geodesics, and can be interpreted as the momentum component of the particle along the direction of the Killing vector field in space-time.

Sebastian Riese
  • 11,682