Magnets And Charges

Question

What is the reason that like charges repel and unlike changes attract each other ? is there something acting in atomic level? Why do charges that are like that donot attract each other ?

Answer 1

What is the reason that like charges repel and unlike changes attract each other?

It's because of the "spinor" nature of such charged particles:

_{GNUFDL spinor image by Slawkb, see Wikipedia}

A spinor is a mathematical entity which is associated with a a spin ½ geometry which in turn is associated with Dirac's belt and the Dirac equation. That's "a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-½ massive particles". It's to do with the wave nature of matter, and whilst these waves aren't actually flat Möbius strips, they are waves, and whilst we say that in atomic orbitals electrons exist as standing waves they aren't truly motionless. We know this because of the electron's magnetic moment and the Poynting vector and the Einstein–de Haas effect which demonstrates that "spin angular momentum is indeed of the same nature as the angular momentum of rotating bodies as conceived in classical mechanics". All in all, a charged particle has an intrinsic spin which makes it what it is, see hyperphysics.

To understand why this results in attraction and repulsion, you have to take careful note of Jackson's Classical Electrodynamics: "one should properly speak of the electromagnetic field F$_{\mu\nu}$ rather than E or B separately". I think the only way to really appreciate this is to try to depict F$_{\mu\nu}$ for an electron. Amazingly you can't find any depictions of this in textbooks. But IMHO you can do it, by combining radial electric field lines with concentric magnetic field lines like this:

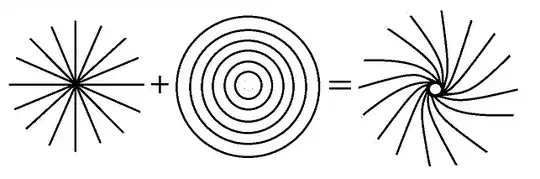
The combined thing on the right looks like it ought to be called a "spinor". It looks like some kind of vortex, which ties in with Maxwell's page title. And you may appreciate that counter-rotating vortices attract and co-rotating vortices repel. In similar vein if you set down an electron near a positron, which has the opposite chirality, they will move towards one another linearly. Then if you throw the electron past the positron they will also swirl around each other, something like this:

This is what we see in positronium, and IMHO it makes the Lorentz force $\mathbf{F} = q\left[\mathbf{E} + (\mathbf{v} \times \mathbf{B})\right]$ look totally obvious. It's just a combination of the linear and rotational force that results from two dynamical "spinor" electromagnetic fields interacting. I think it's all really simple once you get an intuitive picture of what spinors are all about. There is no magic, and no mystery either.