Calculate Spring Constant

Question

I am editing the question because it was misunderstood to be a homeowrk question.

I am modeling a Stumps equipment for a game called Cricket.Typically the game consists of 3 wooden stumps positioned upright by hammering them into the ground.They were setup behind the batsmen,batter in baseball analogy.The pitcher scores a point if he was able to hit the stump and causing it to move.For the stump to move,i.e to overcome the static friction, he should be throwing atleast at speed of 10mph.

The inverse conical section at the base of each stump,in the left side of the image, is not seen in the middle image because it was hammered into the ground.

Sometimes it is played for recreation on a concrete ground like a tennis court.So there is no possibility of standing them upright by hammering into the concrete.So I am planning to design an equipment similar to the one like the right side of the image.

The side with the spring will be facing the wicketkeeper standing behind the batter,in the picture above.The movement of the stump is restricted by the spring connected to each of them.

My problem is to find the right type of spring which restricts the movement the same way as the ground resists the movement of the stump when hammered into the ground.The gound resists the stump from moving for balls hitting less than 10mph.The spring should be behaving the same way.

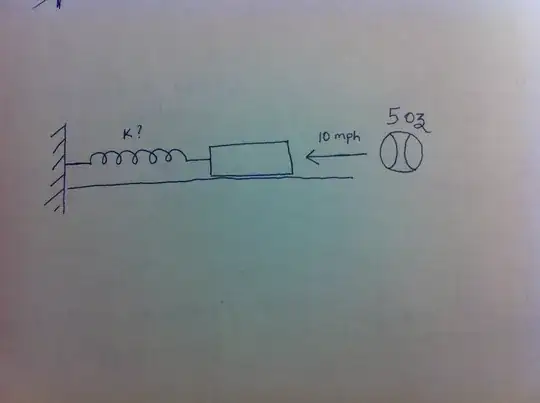
The picture shown below has a ball of 5 oz hitting the brick of negligible mass,negligible static and kinetic friction,resting on the table,connected to a spring.The brick is placed just to make sure the ball has sufficient surface area to make contact.

For the ball to cause a compression in spring ,it should be travelling at least 10 mph.I would like to know the initial tension and the spring constant of the spring.

A simple analogy to this problem would be to compute the static friction of a brick resting on a surface when it takes a ball of 5 oz traveling at 10 mph to overcome static friction.In my case I need the spring constant or initial tension instead of static friction.

Let me know if I am not clear

Answer 1

I cannot comment on the full design because the question is lacking on details, but I can explain more about the situation where you hit a mass with a ball and a spring reacts to it (like the sketch shown)

1. Consider the friction force as $f=\mu m g$ and the equations of motion $$m \frac{{\rm d}^2x}{{\rm d}t^2} + k x \pm f = 0$$ _{The sign of $f$ depends on the direction of motion, but since I only consider what happens initially I have to use the $+f$ side.}

2. The general solution given initial conditions $x(t=0)=X$ and $\dot{x}(t=0)=V$ is $$ x(t) = X \cos(\omega t) + \frac{V}{\omega} \sin(\omega t)+ f \frac{\cos(\omega t)-1}{m \omega^2} $$

3. The frequency of natural oscillation $\omega$ is critical to the solution and for a simple mass spring system it is $$\omega = \sqrt{\frac{k}{m}}$$
4. Use the natural frequency to estimate the average impact time. A full cycle occurs during time $$\Delta t = \frac{2 \pi}{\omega}$$
5. The collision with the ball causes a momentum transfer (impulse) that equals with $$J = \frac{ (1+\epsilon) v_{ball}} { 1/m+ 1/m_{ball} } $$
6. The average force of impact is $$F_{ave} = \frac{J}{\Delta t} = \frac{(1+\epsilon) \omega v_{ball}}{2 \pi \left(\frac{1}{m}+\frac{1}{m_{ball}}\right)} $$ where $\epsilon <1$ is the coefficient of restitution. If the ball doesn't bounce back a lot make it small, close to zero; if it bounces back very elastically, it approaches one.
7. Finally set the average impact force to friction $f$ at $v_{ball}$ $$ \omega = \frac{2 \pi \mu g (m+m_{ball})}{(1+\epsilon)m_{ball}v_{ball}}$$ and find the spring stiffness by $$k=m \omega^2$$

_APPENDIX

For a slender beam of diameter $d$ the 1st natural frequency is $$\omega_1 = \frac{4.73^2}{4} \frac{c d}{\ell^2} $$ where $c$ is the longitudinal wave speed and it calculated by $c^2 = \frac{E}{\rho}$. The $i$-th frequency is $$\omega_i = 0.1103 (2i+1)^2 \omega_1$$

The impact calculation needs adjusting a the effective lumped mass of a slender beam of length $\ell$, mass $m_{rod}$ when impacted a distance $c$ from the center of mass is: $$m = \frac{\ell^2}{\ell^2+12 c^2} m_{rod}$$