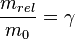1

This question made me curious. It refers to a ball which is rotating so that its equator is approaching the speed of light, then talks about what it would look like if the observer moved. What I'm curious about is if the ball itself could move much at all. If the edge is already moving very near the speed of light, would its rotation have to slow down for the whole ball to accelerate significantly in any direction?

For clarification, the way I'm thinking of this is that you'd have a ball (made of unobtanium - this questions isn't about whether or not it's possible) spinning so that the top speed of any point on it is very close to $c$ and otherwise not moving. Then you give it a strong shove (parallel to a line from its center to the "equator" of spin, for simplicity) while it continues to spin. Then, instead of all points along its equator moving at an equal speed, the side spinning towards the direction of travel would be changing position faster than the side spinning away from that direction. Assuming your shove was strong enough, that could push the forward-spinning edge across the speed of light.

Of course that can't happen, so the question is what would happen? Would the spin of the ball need to slow down to compensate, so that no part of it travels faster than $c$? Would it resist being pushed at all, the same way a gyro resists when you try to move it? Something else entirely? Am I even envisioning the physics of it correctly? If not, please give an explanation of where my reasoning is wrong.

Community
  • 1
thanby
  • 531
  • What does "a significant amount of inertia" mean? I don't understand your question. Any addition of translational velocity to the ball would simply be a Lorentz boost. The equator will still be moving less than $c$ for all inertial reference frames. – Bill N Sep 24 '15 at 15:15
  • I guess the inertia part didn't make sense now that I think about it. It's been removed. Can you give a little explanation of the Lorentz boost? – thanby Sep 24 '15 at 15:20
  • Is this ball accelerated parallel to its spinning axis, or parallel to some line from the center of the ball to the equator of the ball? – stuffu Sep 24 '15 at 19:48
  • Parallel to a line from the center to the equator, thanks for helping me clarify – thanby Sep 24 '15 at 20:28
  • Trying to piece this together from the information here I think if the disk rotation is fixed near the speed of light then any force applied to the center would cause the disk to exchange mass for energy. Maybe there is a tendency to reduce rotation speed rather than exchange mass for energy. – Eric Roper Apr 04 '17 at 06:15

3 Answers3

1

Revolutions per minute as measured by any clock attached to any part of the ball will be unchanged.

A clock on the equator will be experiencing varying time dilation after the push, in the frame where the ball has linear motion. A clock on a pole will experience just the most basic time dilation in the frame where the ball moves linearly.

Linear motion must not cause any accumulation of time difference between a clock on the equator and a clock on a pole. Generally a spinning ball must not be an detector of absolute linear motion.

If a clock on the equator measures how much time it spends on the left side of the ball and on the right side of the ball, the result must be that the times are equal.

If an observer in the frame where the ball has linear motion measures how much time a clock on the equator spends on the left side of the ball and on the right side of the ball, the times are not the same. The ratio of times spend on the left side and the right side must be the same as the ratio of time dilations on the left side and the right side.

(Please somebody edit this ;) or tell me what to say instead of "left side" and "right side")

A short answer: It is possible to use a spinning ball as a clock. A spinning-ball-clock time dilates like clocks do.

stuffu
  • 1,978
  • 11
  • 11
1

Of course that can't happen, so the question is what would happen? Would the spin of the ball need to slow down to compensate, so that no part of it travels faster than c? Would it resist being pushed at all, the same way a gyro resists when you try to move it? Something else entirely? Am I even envisioning the physics of it correctly? If not, please give an explanation of where my reasoning is wrong.

In this unnatural setting (where classical electrodynamics exists and no cohesive forces with electromagnetic exchanges hold the ball together,) what will be happening as the equator of the ball approaches c and the central parts around the axis, the relativistic mass will be growing the further out from the axis .

Special relativity states for masses moving with a high velocity close to the velocity of light that the inertial mass changes , it is called relativistic mass, given by :

relmass1

a body at rest has the rest mass

relmass2

with the ratio

relmass3

gamma goes to infinity as the velocity approaches c, and in the scenario above that is what will be happening to the density at the rim:

If the ball started with density d grams per centimeter it will become a function, d(r) where r is the distance from the axis. It will be the rotation of a non uniform ball . If a tangential force is applied to increase the outside equator motion, the mass there will grow accordingly to the impulse and a wobble will enter the uniform rotation.

In special relativity the extra energy entering a system when approaching the velocity c turns to mass , due to E=mc^2.

I will note that this is one of the few cases where the concept of relativistic mass is useful, i.e when one applies Newtonian physics where the second law holds with the relativistic mass.

anna v
  • 233,453
  • Are you perhaps assuming that the process of continually turning around is not time dilated in the frame where the turning object also moves linearly? – stuffu Sep 24 '15 at 19:36
  • So what it boils down to is that the harder you "shove" the ball, the more mass its outer edge will gain from the energy you apply, essentially building up a resistance to the push? – thanby Sep 24 '15 at 20:48
  • @user7027 I am not examining time dilation, which will also be "distance from axis" related. I am assuming the ball rotating in its rest frame. I think that is what the question is about. No about moving observers. – anna v Sep 25 '15 at 04:32
  • @thanby yes , approaching the speed of light energy turns to relativistic mass. Look at the force formula in the link, it takes the place of inertial mass in newtonian second law – anna v Sep 25 '15 at 04:32
  • I am trying to follow the logic you provided about injecting additional energy into the system from three different cases. The case of injecting energy tangent to the diameter and perpendicular to the axis of rotation and in the direction of rotation then this would grow the disk so either the push is no longer towards the edge or the injection force moves with growth. If this energy injection were similar but against rotation then this should slow rotation. If this energy injection were in the middle of the disk it would both slow the rotation and add to growth but I think these cancel out. – Eric Roper Apr 04 '17 at 03:36
  • The term “relativistic mass” is obsolete, as it may lead to misconceptions (even among experts), as it is in direct conflict with the kinematical structure of special relativity, and is inconsistent with the geometrical formulation of special relativity — the recommendation from Einstein himself is “Instead of introducing M it is better to mention the expression for the momentum and energy of a body in motion.” – MarianD Jun 30 '19 at 18:59
  • @MarianD as I have said in the answer, the only place where relativistic mass is useful as a concept is where inertial mass is necessary for solving the motion. As will be the case for a spaceship traveling at very high velocities if you want to calculate the fuel needed. – anna v Jul 01 '19 at 03:52
  • @annav, the nineteen-century ether theory was useful, too — it explained almost all, and even predicts the existence of electrons and positrons. Does it mean that we will exploit it in situations where it provides a simpler solution? Already 50 years continues the effort to dissuade the physics community from introducing and using the concept of relativistic mass. Why don't contribute to this in your (future) answers? – MarianD Jul 01 '19 at 09:43
  • @MarianD it so happens that the relativistic mass is mathematically correct within special and general relativity, which the aether is not. If you ever want to calculate how much fuel you will need for a spaceship, it will be simpler to use the relativistic mass.. Whats your problem with that. Nobody in particle physics is using relativistic mass as four vectors have taken over the algebra.. In this question it it relevant because it gives the inertial mass which is a simpler mathematial setting for the problem at hand. – anna v Jul 01 '19 at 10:45
  • @annav, it's your decision to support this misconception. Unfortunately, you are not the only person who justify it, so in your case I give up. – MarianD Jul 01 '19 at 11:13
1

Would it resist being pushed at all, the same way a gyro resists when you try to move it?

Let's say the ball has mass 1 kg when not spinning, and mass 10 kg when spinning.

When that spinning ball is pushed around, it will behave almost like a non-spinning ball with mass 10 kg.

When the spinning ball is pushed around at non-relativistic speeds, one can use Newton's laws to find the approximate trajectory of the ball. $ F=ma $ , where $ m=10 kg $ in our example case.

When the spinning ball is pushed around at relativistic speeds, one can use relativistic mechanics to find the approximate trajectory of the ball. $ F=ma* \gamma ^3 $ , where $ m=10 kg $ in our example case.

There is just a small subtlety: A ball that is spinning and moving linearly does not necessarily behave like it was a more massive non-spinning homogeneous ball, instead it may behave like it was a more massive non-spinning ball whose one side is more massive than the other side.

stuffu
  • 1,978
  • 11
  • 11