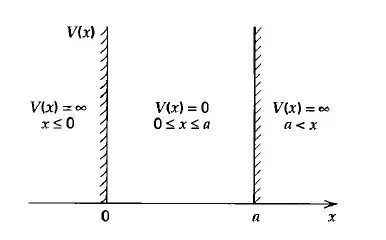
Go back to your time-independent Schrödinger equation:
$$
-\frac{\hbar^2}{2m}\frac{d^2 u(x)}{dx^2}+V(x)u(x)=Eu(x)
$$
This is a differential equation that must be satisfied for all values of $x$. In particular, if we look at the equation for $x = x_0 > a$, we have
$$
-\frac{\hbar^2}{2m}u''(x_0) + (\infty) u(x_0) = E u(x_0)
$$
If $u(x_0) \neq 0$, then at least one of two things must be true: $E = \infty$ or $u''(x_0) = \infty$. We presumably do not want the energies of our eigenstates to be infinite, and we presumably want our wave-functions to have well-defined second derivatives (except perhaps at isolated points.)1 Thus, this is a contradiction, and so we must have $u(0) = 0$ in a region of space where $V(x) = \infty$.
Now, in reality, the infinite potential well should be viewed as the limit of the finite potential well, i.e., take $V = V_0 < \infty$ for $x <0$ and $x>a$ and then take the limit as $V_0 \to \infty$. In such a case, the particle's wave-function would satisfy (for example)
$$
u''(x_0) = \frac{2m(V_0-E)}{\hbar^2} u(x_0)
$$
which has the solution (for $x < 0$)
$$
u(x) = A \exp \left[ \frac{\sqrt{2m(V_0-E)}}{\hbar} x \right].
$$
(There's also a solution with the sign of the square root flipped, but it turns out to be impossible to normalize it.) As $V_0 \to \infty$, we get $u(x) \to 0$ for all $x <0$. Thus, even if we take the limit more carefully, we still get the result that the wavefunction vanishes outside the well as $V_0 \to \infty$.
1 In some circumstances, you can have a function with $u''(x_0) = \infty$ at isolated points; in fact, in this case $u''(0) = u''(a) = \pm \infty$ depending on the eigenstate. But this is only allowable at isolated points, and is really an artifact of choosing a physically unrealistic infinite potential. In reality, potential wells are never infinite, and so the second derivative of the wavefunction is always well-defined everywhere.