Although some problems have been raised in Black Hole Cosmology (movement towards the singularity, past singularity and future singularity problem, the expansion of the universe, etc.), these problems are likely to be solved.
1.Black Hole Cosmology
The Black Hole Cosmology is very likely to hold true if the following four things are true,
1)Finite Universe
We do not yet know whether the universe is finite or infinite. However, in my personal opinion, infinity is a mathematical notion, and there seems to be no infinite in physical reality. Even flat space-time does not guarantee an infinite universe (infinite mass-energy distribution). Since the age of the universe is finite and the propagation velocity of the field is also finite, the mass distribution is considered to be finite. Therefore, if we exclude the infinite universe, we face the problems 2)~4).
2)Schwarzschild's radius equation
If we find the size at which the mass distribution with the average mass density of the present universe forms a black hole.
$R = \frac{{2GM}}{{{c^2}}}$
${R_{UB}} = \sqrt {\frac{{3{c^2}}}{{8\pi G\rho }}} = 14.3Gly$
The above expression means that if the present universe has a critical mass density $ρ_c$ value and the size is approximately $R_{UB}=14.3Gly$ or more, this region becomes a black hole.
3)Observed average density
The order of 5~6 hydrogen atoms per m^3
4)The observable universe 46.5Gly (*the entire universe much larger than the observable universe.)
Currently, we estimate that the size of the observable universe is larger than 14.3 Gly, and the entire universe is estimated to be larger than the observable universe 46.5Gly, so our observable universe inevitably exists inside a huge black hole called the universe.
The Black Hole Cosmology is the inevitable conclusion of the above 4 items.
2) is an equation that has been verified in two different theoretical systems (Newtonian mechanics and general relativity), 3) and 4) is on a very solid foundation, and even if 3) and 4) have some errors, the entire universe is estimated to be much larger than the observable universe. Even if the average density is lower than the current observation, the much larger entire universe inevitably renders the universe a black hole. This is because when the universe becomes R times larger, the density required to become a black hole decreases by $1/R^2$.
2.Weaknesses of the Black Hole Cosmology
1)In a black hole, all matter is compressed into a singularity, so there is no space for humans to live. There is no almost flat space-time that could contain the observable universe inside a black hole.
2)In the black hole, singularity exist in the future, and in the universe, singularity exist in the past. Black hole and the universe are opposites.
3)The universe is expanding. Inside a black hole, all matter must contract at a singularity. The two models show opposite phenomena. It is difficult to explain the expansion of the universe inside a black hole.
Although this objection(or Weaknesses) appears to be clear and well-grounded, in fact, this objection also has its own weaknesses.
1)The proposed weakness does not break the argument 2)~4) of the Black Hole Cosmology. Whatever the weakness , if 1) ~ 4) does not collapse, the Black Hole Cosmology is very likely to hold.
2)Most physicists and astronomers believe that the singularity problem will be solved either using quantum mechanics or in some unknown way, so there will be no singularity.
In other words, in the process of solving the singularity problem, there is a possibility that the singularity problem of the Black Hole Cosmology will also be solved.
3)Since the singularity exists in the Schwarzschild solution, the Schwarzschild solution must be changed for the singularity problem to disappear. That is, among the elements constituting the Black Hole Cosmology, the "2)Schwarzschild radius equation" is affected.
For the singularity to disappear, there must be a repulsive force inside the black hole. Due to this repulsive force, an uncompressed region inevitably exists inside the black hole.
The remaining problem is, "Could an uncompressed region be larger than the observable universe?"
[Solutions to the problems of Black Hole Cosmology]
Weakness 1)In a black hole, all matter is compressed into a singularity, so there is no space for humans to live. There is no almost flat space-time that could contain the observable universe inside a black hole
Solution
1.The singularity problem is known as a flaw in general relativity, and considering the gravitational action of the gravitational field, there is a possibility that the singularity problem can be solved
The fundamental principle of general relativity states that "all energy is a source of gravity". However, the field equation created by Einstein did not fully realize this principle.
The energy of the gravitational field must also function as a gravitational source. Einstein was also aware of this, and for over two years, beginning in 1913, he worked to formulate a field equation that included the energy-momentum of the gravitational field. However, because it was difficult to define the energy of the gravitational field in general relativity, Einstein could not complete the field equation including the gravitational action of the gravitational field. So, the singularity problem and the dark energy problem came into existence.
2.Gravitational self-energy or Gravitational potential energy
For uniform, spherical distribution,
${U_{gs}} = - \frac{3}{5}\frac{{G{M^2}}}{R}$
In the generality of cases, the value of gravitational self-energy is small enough to be negligible, compared to mass energy $Mc^2$. So generally, there was no need to consider gravitational self-energy. However the smaller R becomes, the higher the absolute value of $U_{gs}$. For this reason, we can see that $U_{gs}$ is likely to offset the mass energy in a certain radius.
Thus, looking for the size in which (negative) gravitational self-energy becomes equal to (positive) mass energy by comparing both,
$|{U_{gs}}| = | - \frac{3}{5}\frac{{G{M^2}}}{{{R_{gs}}}}| = M{c^2}$
${R_{gs}} = \frac{3}{5}\frac{{GM}}{{{c^2}}}$
This equation means that if mass $M$ is uniformly distributed within the radius $R_{gs}$, gravitational self-energy for such an object equals mass energy in size. So, in case of such an object, (positive) mass energy and (negative) gravitational self-energy can be completely offset while total energy is zero. Since total energy of such an object is 0, gravity exercised on another object outside is also 0.
Comparing $R_{gs}$ with $R_S$, the radius of Schwarzschild black hole,
${R_{gs}} = \frac{3}{5}\frac{{GM}}{{{c^2}}} = \frac{3}{{10}}{R_S}$
This means that there exists the point where negative gravitational self-energy becomes equal to positive mass energy within the radius of black hole, and that, supposing a uniform distribution, the value exists at the point $0.3R_S$, about 30% level of the black hole radius.
In case of the smallest stellar black hole with three times the solar mass, ${R_S} = 9km$. $R_{gs}$ of this black hole is as far as $3km$. In other words, even in a stellar black hole with smallest size that is made by the contraction of a star, the mass distribution can't be reduced to at least radius 3km.
3.Black hole does not have a singularity, but it has a Zero Energy Zone
From the equation above, even if some particle comes into the radius of black hole, it is not a fact that it contracts itself infinitely to the point $r=0$. From the point $R_{gs}$ (or $R_{gs - vir}$), gravity is 0, and when it enters into the area of $R_{gs}$ (or $R_{gs - vir}$), total energy within $R_{gs}$ (or $R_{gs - vir}$) region corresponds to negative values enabling anti-gravity to exist. This $R_{gs}$ (or $R_{gs - vir}$) region comes to exert repulsive gravity effects on the particles outside of it, therefore it interrupting the formation of singularity at the near the area $r=0$.
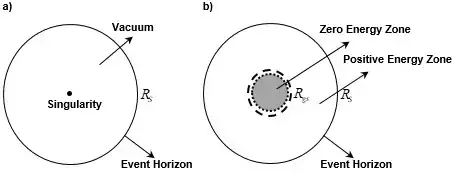
Fig.1. Internal structure of the black hole. a)Existing model b)New model. If, over time, the black hole stabilizes,the black hole does not have a singularity in the center, but it has a zero (total) energy zone.
4.Inside a sufficiently large black hole, there is enough space for intelligent life to exist
A black hole has no singularity, has a Zero Energy Zone with a total energy of zero, and this region is very large, reaching 15% ~ 30% of the radius of the black hole. Inside a sufficiently large black hole, there is an area where intelligent life can live.

For example, if the masses are distributed approximately 46.5Gly with the average density of the current universe, the size of the black hole created by this mass distribution will be 491.6Gly, and the size of the Zero Energy Zone will be approximately 73.7Gly ~147.5Gly. In other words, there is no strong tidal force and a region with almost flat space-time that can form a stable galaxy structure is much larger than the observable range of 46.5 Gly. The entire universe is estimated to be much larger than the observable universe, so it may not be at all unusual for us to observe only the Zero Energy Zone (nearly flat space-time).
Weakness 2)In the black hole, singularity exist in the future, and in the universe, singularity exist in the past. Black hole and the universe are opposites
Solution
Just because a singularity exists in the future in a black hole and a singularity in the universe in the past does not negate the Black Hole Cosmology.
In order to solve the singularity problem of black hole, there must be a situation in which repulsion outweighs attraction (gravity) below a certain size. In a situation in which repulsion outweighs attraction, the area must expand. If this expansion is converged into the past, a singularity appears, and thus the singularity direction becomes a form that exists in the past.
In a stellar black hole, an object enters the black hole from the event horizon, and in the case of the universe, it is only a case of expanding from a singularity toward the event horizon. It is still a phenomenon that occurs inside a universe black hole.
When an object is thrown upwards in Earth's gravitational field, it looks different when it rises up and when it comes down from its apex, but both events are just two aspects of a single event in the same gravitational field.
Weakness 3)The problem of cosmic expansion inside a black hole. The universe is expanding. It is difficult to explain the distance between galaxies inside a black hole
Solution
There are several ways to explain the expansion of the universe inside a black hole (formed when only mass energy is considered without considering gravitational self-energy).
Consider the initial state of the universe. The entire universe is larger than the present observable universe, $46.5Gly$. Since we do not know the size of the entire universe, after thinking about the state in which all the mass-energy in the present observable universe is concentrated in a very small area, let's apply this logic to the entire universe.
As calculated above, the size of the ZEZ produced by all mass-energy in the observable universe is approximately $73.7Gly$ ~ $147.5Gly$, and the size of the universe black hole is $491.6Gly$. Since these materials are concentrated in a very small area, the negative gravitational potential energy of this area exceeds the positive mass energy and corresponds to a negative mass state as a whole. The negative gravitational potential energy acts as a repulsive force on the positive masses, so it expands.
This expansion is accelerated up to at least ZEZ ($73.7Gly$ ~ $147.5Gly$), and since it is in an accelerated state, expansion continues beyond ZEZ. As time passes, when the distribution of mass is outside the ZEZ, the mass state within the ZEZ is a state in which the positive mass energy is greater than the negative gravitational potential energy, so the total mass (within the ZEZ) is a positive mass, and the attraction is applied to the masses outside the ZEZ. This will have the effect of slowing the expansion.
The universe expansion at the time of the big bang is because all matter inside the cosmic black hole started in a region smaller than the ZEZ, and there is a possibility that it corresponds to the accelerated expansion process up to the ZEZ. The size of the ZEZ created by the mass distribution of the observable universe is $73.7Gly$ ~ $147.5Gly$, but the present observable universe is passing $46.5Gly$.
When considering the expansion in the early high-density state of the universe, there is a problem that people mistakenly think that this event is the escape of matter from the inside of the black hole created by the total mass of the universe to the outside to form galaxies or stars.
The black hole event horizon created by the total mass of the universe is very large compared to the area where the total mass of the universe is gathered. In this case, the black hole refers to a black hole formed by considering only mass-energy without considering gravitational potential energy. In other words, in the Black Hole Cosmology model, matter does not escape the universe black hole, but has not yet reached the event horizon of the universe black hole (formed when only mass energy is considered without considering gravitational potential energy).
Refer to my paper: Problems and Solutions of Black Hole Cosmology

