What is the speed of gravity in a Schwarzschild metric?

Question

The question "How does gravity escape a black hole?" has been asked, but the responses are not fully satisfying. Frederic Brunner gives a startling intuitive answer: "Gravitational attraction ... is due to curvature of spacetime outside the black hole. For a black hole to attract something, nothing has to propagate from inside the event horizon." This answer, however, may not be correct, as I will show from a reductio ad absurdum argument below:

Brunner's idea that attraction is due to curvature outside the black hole should generalize to Schwarzschild metrics for objects other than black holes. This would mean that the gravitational attraction of, say, a planet does not emanate from its mass, but is already present in the space outside the mass. In practice then, the effects of gravity in a Schwarzschild metric would be known at infinite speed. Thus, it appears one could send a superluminal message using the oscillating gravitational force from, say, an oblong rotating asteroid, by changing the the frequency of rotation. The amplitude of the oscillation falls off roughly as 1/r**4, but can be detected in principle.

Schwarzschild's metric is stationary, and no information about anything travels anywhere. You should look at time dependent metrics (which are far more complex). Yet, the (mathematical) proof that the "speed of gravity" is the same as the speed of light is constructed by using the Einstein's Field Equation, and not by looking at any particular metric (which must satisfy this equation). — Alexander, Feb 17 '16 at 19:28
Brunner's answer seems to imply instantaneous action at a distance. The metric of a rotating oblong asteroid could be viewed as a perturbation on a stationary Schwarzschild metric. According to Alexander's comment, the Schwarzschild part of the metric would be known instantaneously everywhere, while the perturbation would travel at the speed of light. This is a fair answer. The Schwarzschild metric is an idealization in a universe where nothing is actually stationary, hence instantaneous action at a distance never really occurs. — Karl Pomeroy, Feb 17 '16 at 20:09

score 2 · Answer 1 · answered Feb 17 '16 at 19:37

Your reducio already fails for classical electromagnetism -- particles feel the effects of a static electromagnetic field. When the source charges are moved, this changes the electromagnetic field, but the effects of these changes travel outward from the moving charges at the speed of light. The field here doesn't depend on the charges over there right now, but rather, on the locations of the charges over there at a time (d/c) ago.

It is exactly the same for gravity. Moving a mass distribution creates changes in the metric, and those changes in the metric travel outward at the speed of light. But a test particle dosn't have to know about any of that, it just needs to know the falue of the metric at its location (and in an infinitesimal neighborhood of its location)

To Jerry Schirmer: Yes, my reductio argument was proving something absurd based on Brunner's apparent proposal of instantaneous action at a distance. Alexander's comment, and my response to it, has clarified the confusion. — Karl Pomeroy, Feb 17 '16 at 20:20
This is an interesting paper using the FERMI gamma ray coincidence to limit the velocity of gravitons http://arxiv.org/pdf/1602.04764.pdf — anna v, Feb 25 '16 at 05:18

score -1 · Answer 2 · edited Apr 13 '17 at 12:39

What is the speed of gravity in a Schwarzschild metric?

As far as we know it's the speed of light.

The question "How does gravity escape a black hole?" has been asked, but the responses are not fully satisfying.

I can see this old question. It seems to focus too much on gravitons. Gravity doesn't work because there's particles called gravitons flying back and forth. And electromagnetism doesn't work because there's particles called virtual photons flying back and forth. Magnets don't shine. Hydrogen atoms don't twinkle. Virtual particles are virtual. They only exist in the mathematics of the model.

Frederic Brunner gives a startling intuitive answer: "Gravitational attraction ... is due to curvature of spacetime outside the black hole.

Is this the answer you're referring to? It's more or less right.

This answer, however, may not be correct, as I will show from a reductio ad absurdum argument below: Brunner's idea that attraction is due to curvature outside the black hole should generalize to Schwarzschild metrics for objects other than black holes. This would mean that the gravitational attraction of, say, a planet does not emanate from its mass, but is already present in the space outside the mass. In practice then, the effects of gravity in a Schwarzschild metric would be known at infinite speed. Thus, it appears one could send a superluminal message using the oscillating gravitational force from, say, an oblong rotating asteroid, by changing the the frequency of rotation. The amplitude of the oscillation falls off roughly as 1/r**4, but can be detected in principle.

Your argument is the wrong argument I'm afraid. You should be able to work that out from the rubber-sheet analogy:

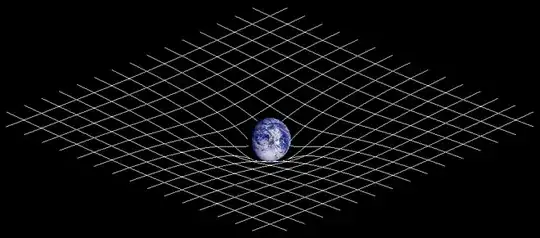enter image description here ^{CCASA image by Johnstone, see Wikipedia}

This plot depicts spacetime curvature. If there was no curvature, the plot would be as flat as a board, and there would be no gravity. The force of gravity at any one location relates to the slope at that location. The tidal force relates to how curved it is at that location, and gravitational time dilation at some location relates to the depth of potential. If you replaced the Earth with a rotating oblong, you would be waving the rubber sheet a little, changing the slope a little, or like Jerry said, "changing the metric". This waving is thought to propagate at the speed of light, but it isn't why an object falls down.

Of course a better analogy would be three-dimensional, rather like this picture, but pushing out rather than pulling in:

enter image description here _{Image credit: Christopher Vitale of the Pratt Institute}

The way it works is that a concentration of energy in the guise of a massive body "conditions" the surrounding space, altering its properties, this affect diminishing with distance. See Einstein talking about it here in 1920: "According to this theory the metrical qualities of the continuum of space-time differ in the environment of different points [20] of space-time, and are partly conditioned by the matter existing outside of the territory under consideration". Google on Einstein elastic. It's rather like space is this gin-clear ghostly elastic continuum. Injecting some mass-energy into the middle of it pressurizes it, the effect diminishing with distance.

What is the speed of gravity in a Schwarzschild metric?

2 Answers2