3

As an aspiring professional bowler, I'm attempting to understand all the factors that influence a bowling ball motion.

The simplest case is when the bowling ball is a uniform sphere and the center of mass is at the geometric center of the ball. (As bowlers, we can and often do drill the ball such that center of mass is offset from the geometric center and such that the inertial tensor has non-zero off-diagonal elements to change the 'ball shape'; eg the path of the ball).

A bowler delivered the bowling ball with an initial velocity and initial angular velocity. The bowling lane is 60 feet long. The first 30 feet is coated with oil such that the coefficient of friction is nearly 0. The last 30 feet has no oil such that the coefficient of friction is greater than 0, but constant, normally 0.20

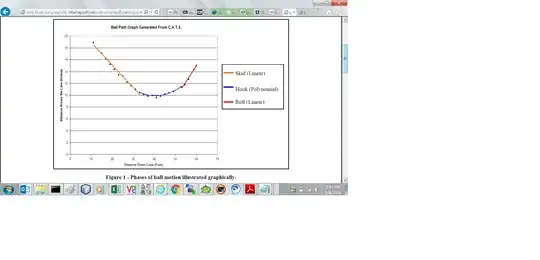
The bowling ball will travel in a straight line in the oil. When it encountered friction at 30 feet, it will then hook and that curve is a parabola. (United States Bowling Congress http://usbcongress.http.internapcdn.net/usbcongress/bowl/equipandspecs/pdfs/articles/skid_hook_roll_v3_final.pdf ).

Why is the hook curve a parabola? Understanding that the path is a parabola will allows the bowler better aim at target 60 feet away.

enter image description here

Articles regarding dynamics of a rolling ball (I wasn't able to understand from these articles why the contact force is constant, resulting in the ball path being a parabola) http://billiards.colostate.edu/physics/Hierrezuelo_PhysEd_95_article.pdf http://biosport.ucdavis.edu/lab-meetings/Frohlich%202004%20What%20makes%20bowling%20balls%20hook.pdf

Jon Doe
  • 53
  • Given the link you give, I suspect that this is driven by simple curiosity more than anything, but the way the question is phrased makes it sound somewhat like a homework/exercise question, and that might get it a poorer reception here than it deserves. Please take a minute to read our guidelines for homework questions, to see how to comply with them if it is, or to distance it from that if it isn't. – Emilio Pisanty Mar 08 '16 at 19:49
  • Not a homework exercise. I'm trying to become a professional bowler, so am trying to understand all the factors influencing ball motion. Will read the guideline. – Jon Doe Mar 08 '16 at 21:27
  • I suspected as much. But the further you can move your question from looking like a formulaic textbook exercise (particularly at first glance), the more likely people will take time with your question. Now also that you can and should upload a screen capture of the graph in that document. – Emilio Pisanty Mar 08 '16 at 22:07
  • Yeah, that's much better. I think it could still have a smoother flow but it's much more clear where you're coming from and what the question is, and that's what matters. Good luck on your answers ;-). – Emilio Pisanty Mar 09 '16 at 00:46

2 Answers2

2

When you throw the ball, you can express the relevant portions of the rotation of the ball as a sum of rotation about two axes - one parallel to the floor (forward motion) and one normal to the floor (sideways motion). The bowling ball is fairly massive, so the angular momentum of the bowling ball about its center of mass does not change much when friction starts to apply after 30 feet, so you can think of the ball as exerting a constant sideways force from its rotation component that is normal to the floor. Constant force equates to constant acceleration, which gives the shape of a parabola.

Ben Bartlett
  • 441
  • If w is the angular velocity, v is the ball center of mass velocity, R is the vector from the center of the ball to the contact point, then friction contact force is umg*R x w - v. This will change v. Likewise, the contact force will torque the ball R x F(contact) = I a, which would also change w. Since both w & v get changed by the contact force, I don't see how the contact force is constant. All the USBC video analysis show the shape is a parabola, so the contact force is constant. I'm just having a difficult time seeing why it's constant given that both w & v changes. – Jon Doe Mar 08 '16 at 21:42
  • 1
    @JonDoe because $w$ and $v$ don't change very much, so the path still closely approximates a parabola. – Asher Mar 08 '16 at 23:07
  • ^This. If you were bowling with a basketball in the same scenario it would not approximate a parabola well for a long distance, but because the bowling ball is so massive, its angular momentum is sufficiently large that it takes friction a long time to change it, so over the length of a bowling lane it remains roughly unchanged. Had the bowling lane been arbitrarily long it would eventually converge to travelling in a straight line. – Ben Bartlett Mar 09 '16 at 19:09
0

Sliding friction is independent of the speed of the sliding. Hence changes in velocity vector and angular velocity vector will not change the magnitude of the sliding friction force.

The direction of the sliding friction force is the difference between the angular velocity to the ball center velocity. Since the ball center velocity is change along this direction, the difference between the angular and ball will remains the same direction.

Thus the sliding friction force has constant magnitude and constant direction, which produce the parabola.

Jon Doe
  • 53