Twin Paradox From Neutral observers perspective

Question

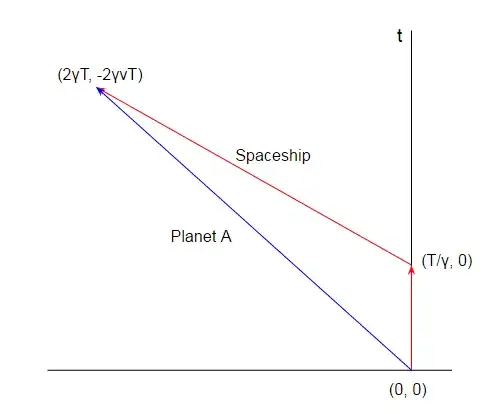
Suppose two planets A & B, with B moving away from A at velocity v.

A spaceship departs from A in the direction of B at velocity v (putting it in the same inertial frame as B), and remains that way for some arbitrary amount of time until turning around and returning.

From A's perspective, the spaceship has been travelling at v, then applied a negative thrust equivalent to 2v thereby decelerating to 0 at the turnaround point, and reversing towards A at speed v until arriving back at A. Thus both legs of the trip have been done with speed v, and the time dilation on both legs should be equivalent.

However, from the perspective of B, the spaceship had an initial velocity of v before even taking off, and after takeoff had decelerated to 0, stayed that way for some amount of time, then accelerated towards A at velocity 2v. Thus on the first leg of the trip no time dilation should have occurred, and on the second leg, the spaceship should experience double the time dilation that A assumed.

If the spaceship recorded time elapsed on its clock on the first leg, and the second leg, will the times differ or not?

Where has my analysis gone wrong?

Note: Let's leave the moment of acceleration/deceleration out the picture. The question could equally have been posed using other travelers (like the Three Brothers version) to avoid acceleration.

Answer 1

For convenience doing the Lorentz transformations let's assume that the planets A and B separate at time zero, and that the rocket launches at time zero. So at time zero all three are at the origin. Now let's identify the key spacetime points in the inertial frame of planet A:

• $P_0: t=0, x=0$ - planet B and the rocket head off at speed $v$

• $P_1: t=T, x=vt$ - the rocket turns round and starts heading back

• $P_2: t=2T, x=0$ - the rocket returns to planet A

So the motion looks like:

If we want to calculate the elapsed time for the spaceship we can do it using the technique described in What is time dilation really? and What is the proper way to explain the twin paradox?, but I won't do this because actually the answer to your question lies elsewhere. Instead let's use the Lorentz transformations to locate our three points in B's inertial frame. Since this isn't rocket science I'll just give the results:

• $P_0: (0,0) \rightarrow (0,0)$

• $P_1: (T,vT) \rightarrow (T/\gamma,0)$

• $P_2: (2T,0) \rightarrow (\gamma 2T,\gamma 2vT)$

So in B's inertial frame the motion looks like:

Note that in B's inertial frame the two legs of the rocket's journey last for different times, which is the resolution to your problem. You are quite correct that A and B disagree about the time dilation experienced by the astronauts on the rocket, but they also disagree about how long the two legs of the journey last. The two effects cancel out so that A and B will agree about the elapsed time on the rocket.

Assuming you looked at the questions I linked you'll know that the elapsed time for a moving object is just the length of its trajectory, and that the trajectory length is the same whatever frame you use to do the calculation. So A and B must agree about the elapsed time on the rocket.