As far as I understand it, a field in physics is a physical quantity that has a value for each point in space and time. However, I'm not sure whether these physical fields that we commonly use (such as gravitational, electric, magnetic) have to be at least continuous, or smooth, or neither.
Firstly, just considering the electric field from a single charged particle (like an electron), there seems to be a discontinuity, because $$E = \frac{C}{r^2}$$ where C is some constant and $r$ is measured as distance from the electron. By the definition of a field, the electric field must also be defined at $r = 0$, (because it is defined at all points in space). So it would seem like there is a discontinuity in the field. I'm not so sure that the $\frac{1}{r^2}$ picture is the whole story however, perhaps some quantum effects save the day?
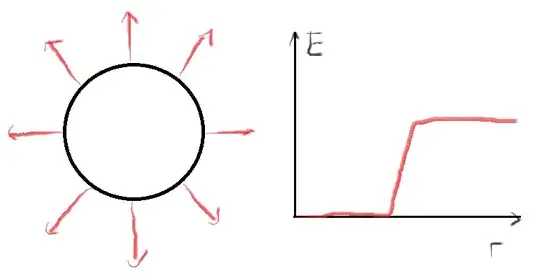
Another example is a hollow charged sphere. The electric field is positive outside the sphere, however on the inside of the sphere it is zero according to Gauss' law. So the graph of the electric field versus the radius is something like the one shown on the right, with $E = 0$ for small values of $r$, a sudden jump at $r = R$ where $R$ is the radius of the sphere, and then the $E$ field should be positive after that.* It seems to me that the curve is definitely not smooth at the boundary, and if I decrease the thickness of the hollow sphere, then it would become rather sharp and jagged.
By these two examples, it seems that physical fields such as electric fields are neither continuous nor smooth, however my gut feeling tells me that they should be both. Is there anything wrong with the examples I chose, or is this the right conclusion? (Or are my definitions of smooth and continuous just nonsensical)
*I messed up the graph a little bit, the $E$ field should decrease after spiking upwards at $r = R$, but that doesn't change my argument