In this video it explains the path of the apple in the general relativity version of gravity as being a straight line on a curved surface. Is this valid?
Edit: this isn't a duplicate of the supposed duplicate. Can verify that by simply reading my question, and reading the other question. What's the point of wasting everyone's time marking fake duplicates? If this question is closed as a duplicate, I'll never post here again.
Yes, the video is an accurate description of the way that relativity describes motion in a gravitational field, and actually I think it's very well done.
However you need to remember that in general relativity it is spacetime that is curved i.e. time is curved as well as space. It's impossible to describe curvature of time in any simple and intuitive way or at least I've never seen any such description in 40 years (!!) studying physics. In fact the motion of falling objects that we see around us every day is mostly due to the curvature in the time dimension.
To go any farther than this gets into some complicated looking mathematics pretty quickly, and while you don't say how much physics you've studied I'm guessing from your question that you're not interested in the gory details. If you've studied Newton's laws of motion you'll know the first law tells us that an object moves in a straight line unless some external force is acting on it. The second law gives us the acceleration of that object as:
$$ a = \frac{F}{m} \tag{1} $$
If there is no force, $F=0$, then we get:
$$ a = 0 $$
which means that the acceleration is zero i.e. the object moves in a straight line at constant velocity (as in Newton's first law).
In GR objects also move in straight lines, and we call these straight lines geodesics. The equivalent of Newton's second law is the geodesic equation:
$$ {d^2 x^\mu \over d\tau^2} = - \Gamma^\mu_{\alpha\beta} {dx^\alpha \over d\tau} {dx^\beta \over d\tau} \tag{2} $$
This looks horrendous, but the left side is basically just an acceleration and the right side is effectively the gravitational force, so conceptually it isn't that different from Newton's second law as in equation (1). The symbol $\Gamma^\mu_{\alpha\beta}$ describes the curvature of spacetime in a complicated way that only we nerds understand! If you're interested $\Gamma^\mu_{\alpha\beta}$ is called the Christoffel symbol.
In flat spacetime the spacetime curvature is zero so $\Gamma^\mu_{\alpha\beta}=0$ and equation (2) simplifies to:
$$ {d^2 x^\mu \over d\tau^2} = 0 $$
and just as with Newton's laws this tells us that the object moves in a straight line at constant velocity in spacetime.
In this video it explains the path of the apple in the general relativity version of gravity as being a straight line on a curved surface. Is this valid?
No. The video delivers a misunderstanding of general relativity. The apple doesn't fall down because of curvature. See Baez:
"Similarly, in general relativity gravity is not really a 'force', but just a manifestation of the curvature of spacetime. Note: not the curvature of space, but of spacetime. The distinction is crucial. If you toss a ball, it follows a parabolic path. This is far from being a geodesic in space: space is curved by the Earth's gravitational field, but it is certainly not so curved as all that!"
Curved spacetime is not curved space and curved time. It's a curvature of the "metric", and metric is to do with measurements. Let's say you placed optical clocks throughout an equatorial slice through the Earth and the surrounding space, then plotted the clock rates. You depict lower slower clock rates as lower down in a 3D image, and higher faster clock rates higher up. So your plot looks like this:
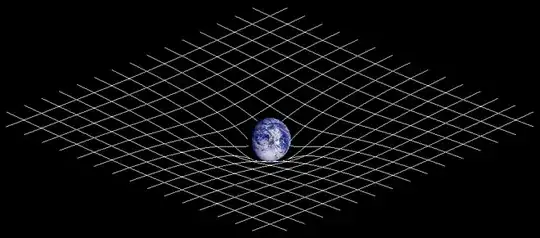CCASA image by Johnstone, see Wikipedia
This is the rubber-sheet picture from the Wikipedia Riemann curvature tensor page. Note that the curvature you can see in this picture relates to the tidal force while the slope relates to the force of gravity. See the tilted light-cones in this Stanford article. The more tilted they are, the steeper the slope, the stronger the force of gravity. Of course the problem with the rubber-sheet picture is that it's tautological, it uses gravity to try to explain gravity. It doesn't explain why light curves. However you can find this in the Einstein digital papers: "the curvature of light rays occurs only in spaces where the speed of light is spatially variable". So light curves like sonar:
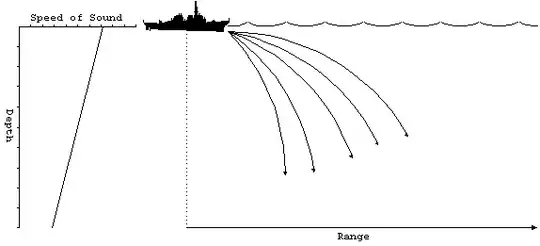
As for why the apple falls down, remember pair production and electron diffraction and the wave nature of matter. Then simplify your apple to a single electron, then simplify that to light going round a square path. What happens to the horizontals? They bend down a little:
So the electron falls down, and it's easy to see why the deflection of light is twice the deflection of matter - only the horizontals curve. For further information see this where Einstein described a gravitational field as a place where space was "neither homogeneous nor isotropic". Also see Inhomogeneous Vacuum: An Alternative Interpretation of Curved Spacetime. It's not unlike what Newton said in Opticks query 20:
"Doth not this aethereal medium in passing out of water, glass, crystal, and other compact and dense bodies in empty spaces, grow denser and denser by degrees, and by that means refract the rays of light not in a point, but by bending them gradually in curve lines?".
