My reasoning is as follows
Atmospheric pressure = $P_{0}$; Spring stretch = $x$; Pressure under top piston = $P$
Balancing forces on top piston
$kx + P S_1 = P_0 S_1$
Balancing forces on bottom piston
$(P+h \rho g) S_2+ mg = P_0 S_2$
Solving the two equations gives
$x= \frac{g S_1(m+h\rho S_2)}{kS_2}$
But the answer in the book is different (below). As I have not considered the forces on the liquid directly, the forces applied by the supports play no role. What am I missing?
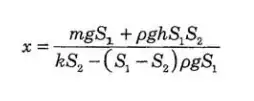
- 71
-
1Hi and welcome to the Physics SE! Please note that this is not a homework help site. Please see this Meta post on asking homework questions and this Meta post for "check my work" problems. – John Rennie May 07 '16 at 05:38
-
This is not a simple "check my answer" type of question. There are conceptual difficulties here when thinking about the role of the supports A and B. – sammy gerbil May 07 '16 at 16:05
-
1Before closing you should have checked that the reasoning of the answer was non-trivial. Conceptual clarity was needed. – santhe May 13 '16 at 08:19
2 Answers
The book answer looks wrong to me. I think $k$ can only appear in combination with $x$, since the tension $T=kx$ in the spring is relevant here but $x$ on its own is not. It could be relevant as a geometrical factor, but there is no length marked $x$ in the diagram.
I agree with your answer - except that you should have $k$ in there with $x$.
I do not think you are missing anything. Judging by the factor $(S_2-S_1)$ in the book answer, it seems that the forces provided by the supports have been taken into account somehow. Like you, I do not think these are relevant. Whatever effect they have will be transmitted through the fluid, and is taken into account by the excess pressure $P$ at the top of the fluid. You have accounted for all of the forces on the upper and lower pistons and correctly balanced them.
So I think the book answer is wrong.
HOWEVER : In the limit of $m\rightarrow 0$ and $S_2\rightarrow 0$ our equation gives the tension in the spring as $\rho ghS_1$. This suggests that the spring is supporting the whole weight of the fluid, and supports $A$ and $B$ have no effect. This does not seem right. In this limit the book answer for the tension is $-\frac{hS_2}{S_1}\rightarrow 0$. This means that the spring is in compression as $S_2$ gets smaller.
On the other hand, when $S_2\rightarrow S_1$ then the supports do not seem to have any effect but the tension in the spring is now $mg+\rho ghS_1$ according to both equations. If we now set $m\rightarrow 0$ our eqn goes to the same limit as before ($\rho ghS_1$) whereas the answer for the book eqn contradicts the result for $S_2\rightarrow 0$. The two situations are effectively the same, so the results should be the same.
So my confidence in our equation remains.
Intuition tells me that the supports ought to play some part in the answer. However, carefully balancing forces on each piston shows otherwise. To paraphrase Sherlock Holmes : "When you have taken into account all of the forces, and carefully balanced them, then whatever result you get, however improbable, must be correct."
FURTHER EDIT TO THIS ANSWER (BY CHET)
The spring actually exerts more tensile force than just the weight of the fluid. This is a direct result of the fact that the pressure throughout the fluid is sub-atmospheric. Here is an analysis of the situation for the case where the mass of the lower piston is equal to zero.
Let $h_1$ represent the distance between the annular region (where the cross section changes from $S_1$ to $S_2$) and the upper piston (this distance is not shown in the figure).
Let's do a force balance on the combination of pistons and fluid:
Downward force on top piston = $P_0S_1-kx$
Upward force on bottom piston = $P_0S_2$
Weight of fluid = $\rho g h_1S_1+\rho g(h-h_1)S_2 $
Pressure at level of annulus = $P_0-\rho g (h-h_1)$. Note that this equation indicates that, at the level of the annulus, the pressure is sub-atmospheric.
Upward force by annular portion of container on fluid = $[P_0-\rho g (h=h_1)](S_1-S_2)$
Force balance on combination of fluid and pistons: $$(P_0S_1-kx)+\rho g h_1S_1+\rho g(h-h_1)S_2=P_0S_2+[P_0-\rho g (h-h_1)](S_1-S_2)$$ Solving this equation for the tension in the spring yields: $$kx=\rho g h_1S_1+\rho g(h-h_1)S_2+\rho g (h-h_1)(S_1-S_2)$$ Notice that the atmospheric pressure has cancelled entirely from this equation. The first two terms on the right hand side represent the weight of the fluid. The third term physically represents the pressure deficit (suction) created by the column of liquid below the annular cross section. If we sum the three terms on the right hand side, we obtain:$$kx=\rho g hS_1$$ This tension is greater than the weight of the fluid itself because of the pressure deficit at the annular cross section.
- 3,161
- 4
- 22
- 53
- 27,277
-
The tension being equal to $\rho g h S_1$ does not mean that the spring is supporting the whole weight of the fluid. If $h_1$ represents the distance between the upper piston to the contraction of area, the weight of the fluid is $\rho g h_1 S_1+\rho g (h-h_1)S_2$. – Chet Miller May 08 '16 at 04:07
-
@ChesterMiller : Thanks for pointing out my slopping thinking. h1 is not specified in the question so I assumed we can set it equal to h. My "however" is a lot of hand-waving. I'm not entirely comfortable with my answer but I don't see anything wrong with santhe's solution. Do you? – sammy gerbil May 08 '16 at 16:56
-
I agree with your assessment. In fact, I gave you an upvote a couple of days ago. – Chet Miller May 08 '16 at 22:55
-
@ChesterMiller : Thank you. I just wondered if you had any insight into the situation that would make me feel more comfortable about my answer, since you answered the santhe's other question so well [ No buoyancy inside liquid, http://physics.stackexchange.com/q/246253]. Like santhe, I wonder if I am missing something. – sammy gerbil May 09 '16 at 00:43
-
Yes. I can help. The thing that was troubling me was not that the spring is supporting the entire weight of the fluid, because it isn't. It is exerting a greater upward force than the weight of the fluid. How can this be? To get a handle on this, please answer this question: The external support AB is exerting an (a) upward force (compressive) or a (b) downward force (tensile) on the container (asuming that the container is massless). – Chet Miller May 09 '16 at 11:44
-
I have made an editorial addition to your answer in order to provide a detailed analysis to explain the physical cause of your consternation. I think this should alleviate your doubts. Please accept my edit. Apparently, since this thread is now on hold, I cannot enter an answer of my own. – Chet Miller May 09 '16 at 23:24
-
@ChesterMiller Thanks to your clear analysis, the problem is solved. If we add the mass m as in the figure and solve as you suggested, the answer is still different than the one given in the book. So I guess it is wrong. – santhe May 13 '16 at 08:14
-
1
I think the book's answer is correct.
Use below free body diagrams and note that $P_2=\rho gh_2$ and $h_2=h+y-x$ and y is lower piston displacement. Also, note that volume of the displaced water for both pistons is equal.

Explanation of the answer:
At first, let’s review the problem description.
We have a container is shown in the question body above. There is water inside the container. The lower piston is fixed by an external force before experiment. The spring is in its free length at this situation. We remove the external force slowly and wait until the system achieves to equilibrium. We want to determine the displacement of the upper piston.
Before solving the problem, I ask a question. Is the problem meaning that the system will achieve to equilibrium for each arbitrary amount of $m$? Also about the other quantities that exist in the problem?
The answer of this question is obviously “No”. In fact, if the system has been achieved to the equilibrium finally; then there have been some conditions those were established before doing the experiment.
Now, let’s draw free body diagram for both pistons.
First, upper piston:
The water doesn’t exert any force to the upper piston except surface tension and cohesion that we neglect them because they aren’t mentioned in the problem body.
Question: why does the water exert no force to the upper piston?
Assume that the upper piston doesn’t exist. So, what was happening? Yes, the water was flowed to the outside of container from narrow pipe. Hence, as the water want to go down (and it is free to go down because the lower piston isn’t fixed), it cannot exert a force to the upper piston in the top direction. The water doesn’t exert a force to the upper piston in the bottom direction too. Because there is no water on the piston. We know that in the stationary liquids, $P=\rho g z$ and for the upper piston we have $z=0$.
Continue the solution:
Considering to the equilibrium of the upper piston, we have:$$kx-P_0 S_1=0\;\Rightarrow\;P_0=\frac{kx}{S_1}$$
It is possible that a question comes to mind: due to the relation above, $x$ only depends on $P_0$ , $S_1$ and $k$ and it is independent of $m$ , $h$ , $\rho$ and $S_2$. This claim is completely correct, of course after doing the experiment!!! In other words, if the experiment has been done successfully and the equilibrium has been established, then we can determine $x$ only by measuring $P_0$ , $S_1$ and $k$. In fact, if the equilibrium has been established, then certainly the problem quantities have been satisfied some conditions. These conditions will appear by checking the equilibrium of the lower piston.
$$P_0 S_2=P_2 S_2+mg$$
In other words, before doing the experiment, we hope that $P_0$ , $S_2$ and $m$ will satisfy the above condition (and if the experiment has been done successfully, so the condition had been satisfied at first certainly), otherwise the experiment will fail and equilibrium will never establish. We want to predict the result of the experiment. So, we must consider to the condition that the experiment will be done successfully under that. For more clarification, assume that the experiment is done successfully for a set of $m$ , $P_0$ and $S_2$. If you change one of these quantities ($m$ for example) and maintain fixed the other two quantities ($P_0$ and $S_2$) and repeat the experiment; the equilibrium will never establish and the experiment will certainly fail.
This question includes two events (position of pistons) that are irrelevant at first view. But I compare it by this example: “Assume that a person has decided to jump from a height. We want to predict that which food he will eat at lunch tomorrow. It is obvious that his food choosing is completely irrelevant with his size or mass also the height of all towers in the world. But we can talk about his tomorrow lunch if he is alive that time and his surviving depends on many thing like his size and mass and also the height of that tower he want to jump from it. So, if he is still alive tomorrow, then we don’t need to check the other factors. But, we are in today and we want to predict the future events. So, we should express the conditions before our prediction.”.
If we continue the solution, we obtain the result that is given by the book.
$$P_0=P_2+\frac{mg}{S_2}=\frac{kx}{S_1}$$ $$P_2=\rho g h_2=\rho g (h+y-x)$$ $$xS_1=yS_2\;\Rightarrow\;y=\frac{S_1}{S_2} x$$ $$x=\frac{\rho g h S_1 S_2+mgS_1}{kS_2-\rho g S_1\left(S_1-S_2\right)}$$
-
I have thought about your solution. I do not understand your explanation of "Why does the liquid exert no force on the upper piston?" I still think that in most cases the liquid does exert pressure on the upper piston. However, this does not affect the final answer. – sammy gerbil May 16 '16 at 00:02
-
To get the book answer you have assumed that the diagram shows the situation BEFORE the spring has extended. The question does not state whether the diagram is before or after extension; assuming it is before is reasonable, and it does give the "correct" answer. On the other hand, if (like Santhe, Chet and I) you assume the diagram is the situation AFTER extension, you get Santhe's equation. The way I read the question, the diagram is the final situation, after extension. So I agree that your revised answer is a good one. It fits the conditions given in the question, which are ambiguous. – sammy gerbil May 16 '16 at 00:10
-
@sammygerbil Thank you very much because of your attention and time. About first comment: Why do you think that the water exert a force on the upper piston? I guess because of Pascal’s Law. But, consider that in this case, the liquid isn’t confined. When you push the upper piston, the water can escape because the lower piston isn’t fixed. I agree that the water will exert a force on the upper piston during the experiment (fluid dynamics) but not after equilibrium establishing (statics). After equilibrium, the water doesn’t exert a force on the upper piston. – lucas May 16 '16 at 04:56
-
@sammygerbil About second comment: My free body diagrams show the situation AFTER extension of the spring i.e. after equilibrium. I couldn’t understand why do you think that they show the situation BEFORE the expansion? Before the expansion, there is no $x$ and you see the $x$ in my free body diagrams:) – lucas May 16 '16 at 04:57
-
Water pressure on upper piston : Suppose mg=0. Then for the lower piston P0=P2=ρgh2. Only one value of h2 is possible (h2=10.3m). Is it possible to have h2<10.3m? Suppose that we remove the top 9.3m from the column of water h2 and replace it with a gas exerting a pressure P1 equivalent to 9.3m of water. Now h2=1.0m and P2=P1+ρgh2 (10.3m=9.3m+1.0m). It does not matter to the lower piston if there is only water above it or water plus gas, provided that the forces balance. The pressure at the top of the liquid is P1 > 0. This pressure can be provided by the upper piston instead of a gas. – sammy gerbil May 16 '16 at 08:45
-
Second comment : I was not referring to your FBDs of the 2 pistons but your diagrams of the whole system. Your last 2 diagrams show the situation before (left) and after (right) the spring has extended. You assumed the diagram in the question is the same as your before (left) diagram. Santhe, Chet and I assumed it is the same as your after (right) diagram. – sammy gerbil May 16 '16 at 08:53
-
@sammygerbil If we replace some of water with a gas, the question will change. It wasn't the same question that was. Gas pressure is different from liquid or solid pressure. Gas pressure is because of its molecules motion mostly and if we neglect its density, its pressure will be uniform. But, in a stationary liquid, the pressure caused because of its weight and it is not uniform. So, if we have a gas in the container, then we have a new question and hence we need to draw new FBDs and use other quantities. – lucas May 16 '16 at 09:56



