I was researching sinusoidal functions when I realized that the wave produced by a wave function looks exactly the same as a light wave. Is a light wave a sinusoidal wave, and can a light wave be described as a sinusoidal function?
-
Maybe a little out of my depth here---I'm no physicist---but I'm pretty sure that the wave functions used to describe photons (and virtually everything else at that scale) are sinusoidal functions. – Solomon Slow Jun 01 '16 at 17:14
-
1Light in general is not necessarily sinusoidal. However, look up Fourier transform. – DanielSank Jun 01 '16 at 17:16
-
1The reason they look the same is because they're both mathematical models at the same idea. No one has ever actually seen a light wave nor can they physically describe one. It's best to describe a "lightwave" as millions of coherent photons radiating outward from the same source. – Bill Alsept Jun 01 '16 at 23:42
3 Answers
A wave is a solution of a wave equation of the form $$\frac{\partial^2\varphi}{\partial t^2}(x,t)=c^2\frac{\partial^2\varphi}{\partial x^2}(x,t),$$ where $\varphi$ is the so-called wave function which represents some "displacement" from the equilibrium. The solutions of this equation are of the form $f(x\pm ct)$. This represents a traveling wave with speed $c$. In particular, a sinusoidal wave $\phi(x,t)=A\sin(kx\pm\omega t)$, where $\omega=kc$ is the wave frequency, is a solution.
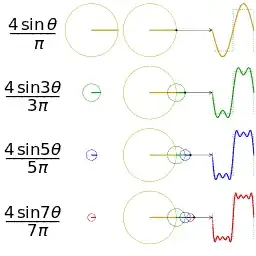
Since the wave equation is linear, it satisfies the superposition principle, so that any linear combination of solutions is still a solution. Hence, $$\varphi=\sum_n \left[A_n\cos(k_nx+\omega_nt)+B_n\sin(k_nx+\omega_nt)\right],$$ is a solution. However when your solution is such a sum of sinusoidal waves with different frequencies the resulting wave can have various shapes, such as a saw-tooth , triangular, square and so on. You can have an idea of this in the gif below, where you are adding up four sinusoidal solutions with different frequencies and getting an almost square solution.
This way of seen an arbitrary wave as a sum of sinusoidal waves is called trigonometric decomposition (or Fourier decomposition accordingly how you compute the coefficients $A_n$ and $B_n$). For a electromagnetic waves the frequency range is continuous so the sums actually corresponds to integrals.
- 17,700
- 3
- 54
- 97
Based on Light Waves
As I am sure you know, a photon (described in wave terms) has both oscillating electric and magnetic field (sine waves) at right angles to each other. Obviously then, if the electric field is drawn vertically , the magnetic oscillating field is drawn horizontal to it.
The field always wants to reach a ground state of zero tension/energy. But once it exists, the energy won't go away, so the field continually fights it, trying to restore itself to zero - and in doing so, overshoots the mark. Now it pulls back in the opposite direction. This repeats forever, and it just so happens that the simplest way of describing this mathematically is as a sine wave. As to why a sine wave and not something else? That's because the reaction of the field to the energy is linear (it's directly proportional to the energy, back towards zero), the energy does not dissipate at any point (there are no losses), the field can't jump arbitrarily between values from moment to moment (the energy transfer of any point in the field carrying the wave behaves smoothly and continuously at every point in time), and it can't jump arbitrarily as you move along the wave either (it's smooth and continuous in the transverse direction of motion).
A Fourier Transform is the mathemathical method of representing the total sum of two or more sine waves. Each of the sine wave, because it is at a different frequency, carries a different amount of energy.
If you have just one sine wave, then you have light of a single frequency.
I've never answered to this website at all, ever. First time.
However, I have worked with waves of all kinds since childhood, including military radar, radio and television waves, light waves, ultraviolet waves, X-rays. Light waves are definitely sinusoidal. That was conclusively determined by James Maxwell. They actually include both sine waves and cosine waves, one being associated with the energy and the other associated with the momentum of the waves. Very similar to water waves.