Diffractive optics in the Fresnel (paraxial) approximation is
exactly the same as the quantum mechanics of a single particle when
thickness along the optical axis is replaced by time, refractive index is
replaced by mass and the inverse angular frequency of the monochromatic
light is replaced by Planck's constant. Here is a brief sketch.
Classical Mechanics
The unity of optics and mechanics is clearest using the generators of canonical transformations (see section 2.1 of Field Theory by Pierre Ramond).
The Hamiltonian for a free particle is $H=\frac{p^{2}}{2m}$. The generator for this Hamiltonian is,
\begin{eqnarray*}
G(q,Q)&=&\frac{m(q-Q)^{2}}{2t}\\
p&=&\frac{\partial G(q,Q)}{\partial q}\\
-P&=&\frac{\partial G(q,Q)}{\partial Q}
\end{eqnarray*}
By messing about with the generator we can write the canonical transformation as a matrix transformation from the initial state $(P,Q)$ to the final state $(p,q)$.
\begin{equation}
\left[
\begin{array}{c}
p \\
q
\end{array}
\right] =
\left[
\begin{array}{cc}
1 & 0 \\
\frac{t}{m} & 1
\end{array}
\right]
\left[
\begin{array}{c}
P \\
Q
\end{array}
\right] \ .
\end{equation}
The $2\times 2$ matrix is an element of the symplectic group Sp(2,R). In other words, classical mechanics (for quadratic Hamiltonians) is synonymous with the two-dimensional defining representation of Sp(2,R) carried on the two-dimensional phase space $(p,q)$,
Quantum Mechanics
The momentum becomes an operator $p\rightarrow -i\hbar\frac{\partial}{\partial q}$. The states become wavefunctions $\langle Q|\psi\rangle$. The canonical transformation becomes a unitary operator,
\begin{equation}
\langle q|U|Q\rangle
\propto \exp\left(\frac{i G(q,Q)}{\hbar}\right)=
\sqrt{\frac{m}{it}}\exp\left(
\frac{im(q-Q)^{2}}{2t\hbar}\right)
\end{equation}
The amplitude $\langle q|U|Q\rangle$ is an infinite-dimensional matrix. The rows are indexed by $q$ and the columns by $Q$.The initial and final states are related by,
\begin{equation}
\langle q|U|\psi\rangle=\int\frac{dQ}{\sqrt{2\pi}}
\langle q|U|Q\rangle\langle Q|\psi\rangle
\end{equation}
The integral is an infinite-dimensional matrix multiplication. Differentiating the above equation recovers Schrodinger's equation,
\begin{equation}
i\hbar\frac{\partial \psi}{\partial t}
=\frac{1}{2m}\left(-i\hbar\frac{\partial}{\partial q}\right)^{2}\psi
\end{equation}
The operator $\langle q|\hat{U}|Q\rangle$ is an element of an infinite-dimensional unitary representation of the symplectic group Sp(2,R). In other words, quantum mechanics (for quadratic Hamiltonians) is synonymous with the infinite-dimensional unitary representations of Sp(2,R) carried on the space of wavefunctions $\psi(q)$.
Ray Optics
Fermat's principle of least time
in ray optics plays the r\^{o}le of the principle of least action in
classical mechanics.
Let $s$ be the distance along a ray.
The time to move by distance $ds$ is $dt=nds/c$ where $c$ is the speed
of light in a vacuum and $n$ is the refractive index of the material.
The total time on the path is,
\begin{equation}
S=\int dt=\int \frac{nds}{c}=\int \frac{n\sqrt{dq^{2}+dz^{2}}}{c}
=\int\frac{ndz}{c}\sqrt{1+\dot{q}^{2}}\ .
\end{equation}
where $\dot{q}=dq/dz$ and the $z$ coordinate in ray optics plays the
r\^{o}le of time in classical mechanics. The Lagrangian in ray optics
is therefore,
\begin{equation}
L=\frac{n}{c}\sqrt{1+\dot{q}^{2}} \ .
\end{equation}
The canonically conjugate momentum is,
\begin{equation}
p=\frac{\partial L}{\partial \dot{q}}
=\frac{n\dot{q}}{c\sqrt{1+\dot{q}^{2}}}
=\frac{ndq}{c\sqrt{dq^{2}+dz^{2}}}
=\frac{n}{c}\frac{dq}{ds}\ .
\end{equation}
The ray optics Hamiltonian is,
\begin{equation}
H=p\dot{q}-L=-\sqrt{\left(\frac{n}{c}\right)^{2}-p^{2}}
\simeq\frac{p^{2}c}{2n}-\frac{n}{c}
\end{equation}
and the last result is for small momentum. Ray optics is the same as classical mechanics with $\frac{n}{c}$ in place of mass $m$. The $2\times 2$ matrices of the defining representation of Sp(2,R) are the ray transfer matrices in ray optics.
Diffractive Optics
The momentum becomes an operator $p \propto -i\frac{\partial}{\partial q}$.
The constant of proportionality cannot be Planck's constant $\hbar$ because the dimensions are wrong. In ray optics, the momentum
has dimensions of second/metre and so the constant has to
have dimensions of second. The physical quantity with dimensions of second
is the inverse frequency of the light. A factor of $2\pi$ appears just
as in Planck's constant $\hbar$ and so the constant with dimensions of
second is, in fact, the inverse angular frequency $\omega^{-1}$ of the
light. The momentum operator is now,
\begin{equation}
p= -i\omega^{-1}\frac{\partial}{\partial q}
\end{equation}
and everything in the quantum mechanics of a particle goes over to
diffractive optics by replacing $\hbar\rightarrow \omega^{-1}$.
For example, the plane wave in quantum mechanics is,
\begin{equation}
\psi(q)=\exp\left(\frac{ipq}{\hbar}\right)
\end{equation}
and so the plane wave in diffractive optics is,
\begin{equation}
\psi(q)=\exp\left(\frac{ipq}{\omega^{-1}}\right)
=\exp\left(\frac{in\omega}{c}\frac{dq}{ds}q\right)
=\exp\left(\frac{i2\pi n\sin(\theta)q}{\lambda}\right)
\end{equation}
using the definition of the ray optics momentum.
Quantum mechanics is not so strange because it is the same theory as diffractive optics in the Fresnel (paraxial or small momentum) approximation. I first learnt this from reading the introductory chapter of "Symplectic techniques in physics" by Victor Guillemin and Shlomo Sternberg.
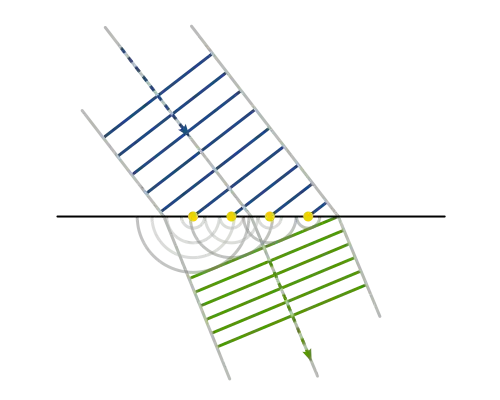
Huygen's Principle and Quantum Mechanics
The amplitude $\langle q|U|Q\rangle$ for a free particle given on the RHS of the first equation of the section on quantum mechanics is a cylindrical wave centred at coordinate $Q$. The integral in the second equation is then a sum over cylindrical waves and this is Huygen's Principle. So, Schrodinger's equation can be derived from Huygen's principle.