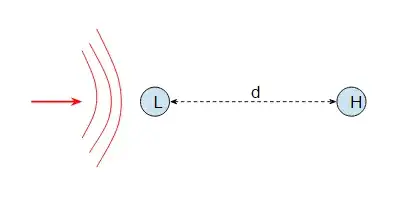
How did a gravitational wave travel from Livingston, Louisiana to Hanford, Washington in 7 milliseconds, when they are separated by 10 milli-light seconds (3002 km)?
Asked
Active
Viewed 3,223 times
2 Answers
60
The time delay depends on the direction the wave is travelling. If it is travelling along the line connecting Livingston and Hanford then the delay time would indeed be the Livingston-Hanford distance divided by $c$:
However suppose the wave was travelling normal to the line connecting the two detectors. In that case the wave would arrive at both of them at exactly the same time and the delay would have been zero:
So the delay can be anything from zero up to $d/c$ depending on the direction the wave is travelling. The only real upset would be if the delay was greater than $d/c$ as that would mean the wave was travelling slower than light.
John Rennie
- 355,118
-
2Which is why we really want more detectors. We'd like to know the direction of the wave as well, but it can move in any direction in 3D space (so 2 degrees of freedom) and we cannot deduce that direction from just one time difference. The example above works because it's flat (2D, one degree of freedom). – MSalters Jun 15 '16 at 08:10
-
2@JohnRennie A live only webcast? So strange. – Yakk Jun 15 '16 at 14:44
-
@Yakk: the paper is on the phys rev lett site here – John Rennie Jun 15 '16 at 18:29
16
It didn't. The key is that the wave is not point-like, it has an extended "wavefront". The wavefront/event just arrived at the two locations with that delay, which gives some information about its direction. You might also be interested in: Is it really possible to break the speed of light by flicking your wrist with a laser pointer?, which discusses qualitatively similar ideas.
