What is a standing wave?

Question

I'm a highschool sophomore, bear this is mind when answering this question, in other words, the answer doesn't need to be in total layman terms, but it should be understandable by an applied highschool student.

1. I have no idea what a standing wave is. Please, explain?

2. Bonus question: How is a standing wave related to the atomic orbit? It is my understanding that the atomic orbit is a mathematical function that describes the probability of an electron being at a certain place, but it is also the image of this function in terms of real space, (i.e. the actual 3 dimensional volume around the nucleus that a particular electron calls "home").

Answer 1

An animation is worth a million words:

Answer 2

This will be a purely mathematical treatment. It needs to be combined with some practical playing around to really "get" it.

---

Traveling wave

Let's start with the description of a harmonic traveling wave in one-dimension. Here "harmonic" just means the mathematical form of the wave is sinusiodal in both time and space.

For concreteness we'll using talk about some kind of transverse matter displacement wave. A wave on a string, perhaps.

The mathematical expression for the displacement of a bit of string away from it's resting position is $$ y(x,t) = A \cos(k x - \omega t) \,.$$ Here $k = 2 \pi/ \lambda$ is the wave-number, $\lambda$ is the wavelength, $\omega = 2\pi/T$ is the angular frequency and $T$ is the period. Most people find it easier to think about wavelength and period, so you might be more comfortable thinking of that as $$ y(x,t) = A \cos\left(\frac{2 \pi}{\lambda}x - \frac{2 \pi}{T} t\right) \,.$$ In either case this represent a continuous sinusoidal wave-train of amplitude $A$ moving to the right as time passes. Replace the $-$ with a $+$ in the argument to the cosine and the wave moves left instead.

The wavelength can have any value you want.

Standing wave

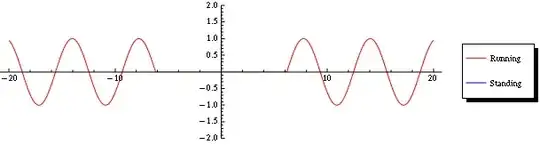
Now we consider the situation with two such wave-trains one moving in each direction. We get \begin{align*} y(x,t) &= A \cos(k x - \omega t) + A \cos(k x + \omega t) \\ &= A\left[ \cos(kx)\cos(\omega t) + \sin(kx)\sin(\omega t) \right] + A\left[ \cos(kx)\cos(\omega t) - \sin(kx)\sin(\omega t) \right] \\ &= 2A \cos(kx)\cos(\omega t) \end{align*} The wavelength is the same and the period is the same, but the behavior is markedly different. The combined spatial and temporal dependence we saw before has been split apart into two separate dependencies. The bumps on the cosine curves no longer move as time passes, instead they stay right where they are and their amplitude rises and falls.

That's a standing wave.

The wavelength is still arbitrary.

To be completely general we have to work the math with a arbitrary phase shift or allow some sine terms as well, but that complexity doesn't teach us anything new.

Standing wave in a confined space

OK. Let's think about a guitar or other stringed musical instrument. Pitch is related to frequency $f = 1/T$, and when I strike a particular string I get a particular note instead of an arbitrary frequency. More over, when I fret up and strike the string I get a different (higher) note.

There has to be something about holding the ends of the string at rest that forces the string to pick some frequency (or rather a set of frequencies).

And that is related to the wave waves reflect. When you send a single pulse down a taunt string at a point where it is rigidly attached, the wave pulse gets sent back to you upside down. It's reflected and inverted. When you pluck a string that sends pulses in both directions and they get reflected, cross the string get reflected again and so on. The system is not lossless so the energy dissipates in time, but for a while there are a set of chaotic vibration on the string. The ones that last are the ones where the spatial wave fits between the ends with a node (zero) at both ends.

The image shows the three lowest frequency modes. The red lines represent the state of the system at time zero and the blue line the state after one half of a period. The gray lines represent other times. (Image original to the author.)

After a short time the string is moving in a pattern that is composed of standing waves (those inverted reflections, right) whose wavelength fits neatly. The equation is $L = \frac{2n-1}{2}\lambda$ where $L$ is the length between the fixed ends and $n$ a counting number (1, 2, 3...).

When you fret the guitar, $L$ gets smaller, so the associated wavelength must as well, but wavelength is related to frequency by the speed $c$ of wave propagation on the string $\lambda f = c$, so when the wavelength goes down the frequency goes up and you hear a higher pitch.

Electron in an atom as standing wave

In the (very wrong) Bohr model, the electron is envisioned as following a circular orbit. In that case an integer number of wavelengths would have to fit around the circle for the electron to not interfere with itself.

That's not a great model, but it is more or less the best you can do until you are ready to tackle three dimensional standing waves in spherical coordinates, so it is where I'm going to leave you.

In reality the electrons aren't little balls and they are not following path (circular or otherwise), and we call the states they occupy "orbitals" rather than "orbits" in part to remind ourselves of those difference.

Answer 3

how is a standing wave related to the atomic orbit (It is my understanding that the atomic orbit is both a mathematical function that describes the probability of an electron being at a certain place, but it is also the image of this function in terms of real space, i.e. the actual 3 dimensional volume around the nucleus that a particular electron calls "home").

If you're new to quantum mechanics, the probability densities of an electron in an atom (e.g. a hydrogen atom) are not the best place to start your enquiry.

A much simpler but quite analogous and insightful system is the particle (e.g. an electron) in a 1D atomic sized box. All information we can have about this particle is contained in its wave function $\Psi$, which is obtained by solving the relevant Schrödinger equation.

Visit the link to see the similarity between the wave functions ($n=1,2,3,...$) and the standing waves depicted in the answer by 'heather'.

Provided the wave function is Real, $\Psi^2(x)$ represents the probability density distribution of the particle over the domain of the box.

For now it's better to see the similarity described above as an analogy, rather than an identity: wave functions of bound particles are not exactly standing matter waves.

Answer 4

A standing wave is basically two opposing waves of equal amplitude, as shown in the diagram below (where n is a positive integer):

You can see this more clearly if you look at the top line where n=3, and follow it as it goes down, up, down. That's wave one. Then, if you look at the bottom line in the same case as it goes up, down, up, that is the opposing wave.

Standing waves can occur with light, x-rays, water waves, sound waves and seismic waves.

You can learn more about standing waves here.

For the bonus part of your question, see the answers for this question on the physics.SE site.

Hope this helps!