Why is interference there when pulses do not overlap in space and time?

Question

Why is there interference present between the two pulses when looking at the spectrum, if they clearly do not overlap in time, and assumingly in space as well (since $x=ct$)?

The spectrum is detected by a CCD coupled to a spectrometer and the repetition rate of the two pulses is about 125 kHz (this two pulses hit the CCD matrix 125000 times per second). Let's say the pulse duration is about 50 fs (which means, they are 15 um in length). Let's say separation between two pulses in time is about 1 ps, which corresponds to the separation in space ~300 um. They clearly never "see" (overlap with) each other when travelling to the spectrometer. However, the interference is there...

Some clarification. The spectrum shown above is a combined effect of the presence of both pulses. The spectra of the individual pulses (when one of the pulses is blocked somewhere in the optical setup, leaving the presence of only the other pulse) are shown below. So the pulses are almost the same, and the difference is in amplitude.

Answer 1

This is a very good question, because we like to think of spectrometers as black boxes, and indeed as seen from the outside there are only two clearly separate pulses going in, so how do they manage to interfere? The answer is clearest by turning the paradox on its head: whatever the interferometer is doing, it needs to be coherently combining the signals from the two pulses, and it needs to be manipulating them in a way that they coincide in space and time.

---

There's one clear, fundamental way to see that the pulses are simply not as clearly separate as you think. As you well note, if the pulses are separated in time by a delay $T$, the spectrum will oscillate with a crest-to-crest separation of $1/T$. To be able to see this interference, however, you need to be sampling in frequency space at a higher resolution, i.e. your spectrometer needs to be able to distinguish between signals that are separated by $\frac{1}{2T}$ in frequency.

In particular, that means that the observations need to be taking at least a time $2T$, to comply with the time-bandwidth theorem: your spectrometer needs to be interacting with the pulses, in a coherent way, for at least that long. This means that what you thought was a long separation between the pulses isn't all that long at all, and as far as the spectrometer goes they are actually within the same time bin.

---

Going beyond this sort of fundamental observation is a bit hard, because the term "spectrometer" is spectacularly broad, and it covers an enormous range of devices that interact with the signal in different ways, and each of them will comply with this fundamental long-coherence-time requirement in different ways. (In fact, you've made it clear that you're thinking about light, but the same paradox applies to e.g. RF in a wire, or pressure waves in a pipe, so the answer also needs to apply to those contexts.)

However, it is very, very hard to think about this in general abstract terms, so let me exemplify this with a couple of examples, one of them relatively general and one of them more specific to light.

• To kick off, let me produce an abstract model of a spectrometer, which is tasked with measuring the power spectrum of a signal $f(t)$ at a discrete frequency sampling $\nu_1,\cdots,\nu_N$ separated uniformly by a spacing $\delta\nu$.

  I will do this in an abstract fashion, by coupling my signal to a bunch of damped harmonic oscillators with those resonant frequencies, with a graph that looks more or less like this:

  

  Each oscillator can be taking its signal from different points along the pipeline, or all at the same point. For simplicity, assume that each coupling has a negligible effect on the signal.

  Each of these oscillators has an equation of motion of the type $\ddot x_i +\gamma\dot x_i +(2\pi \nu_i)^2 x_i = f(t)$, and each will respond resonantly to signals at frequency $\nu_i$ or within a bandwidth ${\sim}\gamma$ of it. Here $\gamma$ is chosen to be 'small', which means it must be at the order of $\delta\nu$, or slightly smaller.

  In addition to this, there is another crucial ingredient to actually getting the required spectral resolution, and that is the requirement that the observation time $\tau$ be longer than $1/\delta\nu$. If you don't do this, you are kidding yourself that you have reached the resolution you wanted, and there is an easy way to see this: simply feed the system with a tight-bandwidth signal $f(t)=\sin(2\pi\nu_j t)$, and take your measurement at $\nu_i$ to be the amplitude of $x_i$ after a time $\tau$ that is smaller than $1/\delta\nu$ (and therefore also smaller than $1/\gamma$).

  If you do this, the signal will bleed: the neighbouring oscillators, at $\nu_{i\pm 1}$, shouldn't be resonant, but they haven't had time for the amplitude accrued in the first half of the measurement window to cancel out with the amplitude from later on, so you will have a nonzero $x_{i\pm 1}$ and wrongly conclude that your signal had amplitude at $\nu_{i\pm 1}$, which is obviously not what you wanted.

  The experimental procedure, therefore, requires you to let your first pulse through, and even if it has already interacted with all the $x_i$ and left the device, there is a coherent memory of it stored in your collection of oscillators, and you are required to wait a time $\tau > T$ to be able to claim a better spectral resolution than $1/T$.

  If a second pulse comes along within that measurement window, then its contribution to the $x_i$ will add coherently with the amplitude they're already holding. Indeed, it will interfere with it either constructively or destructively in a way that depends on the phase that the $x_i$ have accumulated over the inter-pulse period, giving rise directly to the interference spectrum you plot.

---

• OK, that's nice, but let's make it a bit more explicit by talking about light. Let me borrow this schematic as a representative optical spectrometer:

  

  This spectrometer works by taking our signal as a single point source and collimating it with a mirror, then passing it through a grating, and then using a second mirror to focus the resulting rainbow onto the detector. In this simplified picture, it is very similar to most optical spectrometers out there, and what follows applies very broadly to that class.

  Unfortunately, there is something that tends to get lost when people are discussing this picture, at least at the level of introductory optics textbooks, and it's the fact that this sort of configuration tends to muck about with the temporal details of the pulses. This is normally dropped because it doesn't matter when all you want is an understanding of the optics of the spectrum. However, when we want to look at interference between temporally-separated pulses, then it obviously matters.

  To see what I'm talking about, consider the path taken by the red-light component on the two rays that pass at the extremes of the grating:

  

  The thing to notice here is that the two path lengths are different, with the path on the left being longer. The dot marks the spot on that path where it has the same length as the path on the right.

  This is the crucial insight, because it means that even if I start with a pulse that is localized in time, it will be stretched in time when it gets to the detector, because different parts of the signal for the red detector pixel traverse different path lengths.

  To see this a bit more clearly, let me draw some surfaces of equal time for the different rays involved:

  

  Here I'm plotting circles at equal distance from the source that correspond to rays that go through the two extremes of the diffraction grating, one pair just before the mirror and one pair just before the detector. As you can see, the rays that pass through the right of the diffraction grating come significantly in advance of the rays that pass through the left of the grating.

  This, in turn, has a strong effect on the shape of the pulse. To see this, let me fill in the region between these surfaces with light of the corresponding colour:

  

  (Just to clarify, this is simply a linear fill-in of the different wavelengths, which in essence ignores the curvature of the collimating mirror.) If you then push this forward a bit more, you can get the full temporal evolution of the pulse through the spectrometer:

  

  ^{Mathematica notebook used to produce this animation available through Import["http://goo.gl/NaH6rM"]["https://i.stack.imgur.com/DxUGm.png"]}

  It's important to remark that this is in fact what the pulse will look like spatially, in the regime where you start with a very short pulse. In that case, say, if your pulse lasts 10 fs and therefore has an original spatial width of 3mm, the real-world spatial size of your pulse in the above diagram will be in the range of several centimeters, so your pulse has been stretched significantly. (If your pulse is much longer than that originally, of course, then this will represent a smearing instead.)

  We see, then, that the pulse has been stretched spatially by a fair amount. The next question is, of course, by how much has it been stretched? It should be clear from the diagrams that the amount of stretching increases with the width of the grating, and that for wider gratings the pulse will be temporally stretched more and more.

  This becomes even more relevant when you consider the main reason that we would want a wider grating on our spectrometer which is to get a better wavelength resolution. In other words, if you want to measure with a finer frequency resolution, you need to use measurements that take longer and longer and... well, hello there, uncertainty principle!

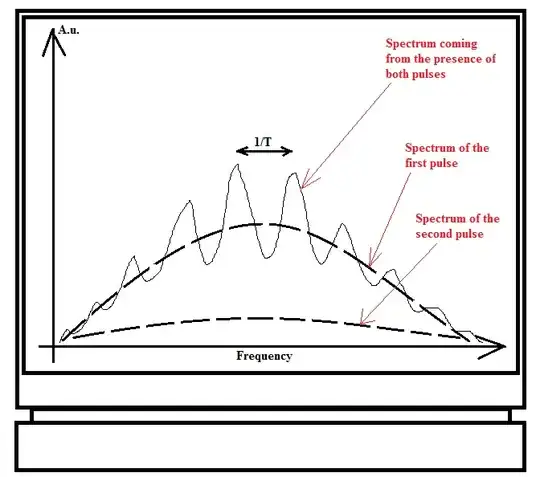
  You can now see where this is going: if you want a spectrometer with enough resolution to resolve the ${\sim}1/T$ interference between your two pulses, then the spectrometer will necessarily stretch the pulses by an amount greater than the inter-pulse separation $T$. This then means that within the spectrometer the two pulses do coincide in both space and time, and it's perfectly reasonable for them to interfere, locally, at each pixel of the CCD detector.

  Pretty neat, huh?

Answer 2

I don't think that the additional chirp inside the detector to overlap the pulses is neccessary to observe the interference pattern in the spectrum.

Each of the pulses consist of many longituidnal EM modes and they are present even if there is no intensity (which occurs due to their mutual destructive interference everywhere expect for the pulse). Therefore, the field of the two beams will interfere also when their pulses do not overlap in time. At least, that's my understanding of this behaviour.