What is the Fermi Surface? I hope this question is not too elementary for this forum, and apologise in advance in case it is.
Allow me to explain my confusion. Given a solid, I believe I have some feeling for the Fermi level. I can understand it, for example, as the characteristic parameter $\mu$ in the Fermi-Dirac distribution of energy levels for the electrons in the system: $$f(\epsilon)=\frac{1}{e^{(\epsilon-\mu)/kT}+1}$$ ignoring for the moment other physical interpretations. Thus, it is the unique energy level that has probability 1/2 of being occupied.
The definition of the Fermi surface, on the other hand, is usually given as 'the iso-surface of states with energy equal to the Fermi level' in the three-dimensional space of wave-vectors $k$, for example in this Wikipedia article:
https://en.wikipedia.org/wiki/Electronic_band_structure
In other words, it is defined to be those $k$ such that $$E(k)=\mu.$$ So far, so good. The problem is, I don't quite understand what $E(k)$ is.
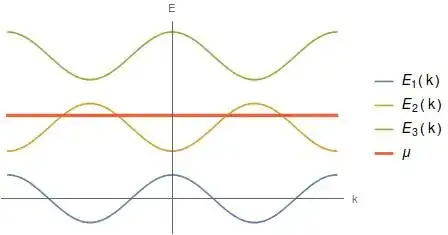
One situation seems to be straightforward, namely a Fermi gas of identical particles. Then $$E(k)=\frac{k^2}{2m}$$ and the Fermi surface is a sphere. However, if we are in an infinite periodic potential, the usual idealised model for Bloch theory, then the solutions to the Schroedinger equation come out in the form $$\psi_{kn}(r)=e^{ik\cdot r}u_{kn}(r),$$ where $u_{kn}$ is a periodic function and $n$ is a discrete index for energy levels. In other words, for each wave vector $k$,
there are many energy levels $E_n(k)$.
So the equation for the Fermi surface would actually look like $$E_n(k)=\mu.$$My question, therefore, is which energy level is the $E(k)$ that occurs in the definition of the Fermi surface? Perhaps there is one Fermi surface for every level $n$? (Assuming that the levels vary continuously over the momentum space, enabling us to consistently index the levels for varying $k$.)
If I could elaborate on my confusion a little bit more, I don't quite understand the definition in this answer to this question:
What is Fermi surface and why is this concept so useful in metals research?
It is stated that
'The Fermi surface is simply the surface in momentum space where, in the limit of zero interactions, all fermion states with (crystal) momentum $|k|<|k_F|$ are occupied, and all higher momentum states are empty. '
For one thing, as mentioned above, for any momentum $k$, there is an infinite sequence of fermion states. The other problem is that I'm not sure that the statement above defines a unique surface, even if I were able to somehow pick out a fermion state $\psi(k)$ for each $k$ that the statement refers to. (I would need to draw a picture to explain this point, which I don't have the competence to do.)