When is it smart to use generalized coordinates?
In my opinion, it depends on your problem's "value" versus the time involved. If you are looking to use a Lagrangian or Hamiltonian, then it's smart.
Generalised co-cordinates are useful in reducing the number of cordinates needed to describe a system to the smallest number.
In the three pictures below:


Source: Generalised Cordinates
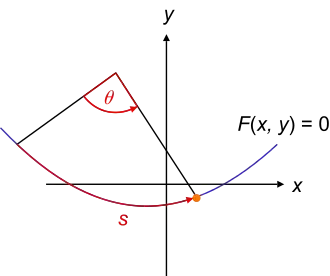
These are curves in 2 D space. We can "get away" with illustrating the path utilising one degree of freedom, (one generalised curve) in each of the cases, since the normal cartesian $x$ and $y$ curves are related to each other and can be parameterized by either an arc length or an angle.
And what are some analytical examples that are too messy to answer without generalized coordinates?
I am not being glib or patronising (because my knowledge of classical mechanics is not great), if you have to ask then you need to use them, if you can, and you need to choose carefully, although the constraints involved well, they will ahem....constrain you in your choice.
We can impose constraints on position coordinates related to a rigid body, consisting of a large number N of particles. By the rigid nature of the body itself, a constraint is automatically imposed on the otherwise independent nature of the component parts. In effect, this means we have the ability to locate/specify the position coordinates of every particle by only having 6 specified quantities, the $X,Y, X$ of the CM, and the three Euler angles $\phi$, $\theta$ and $\psi $.
If we go further and allow the position of the CM to be fixed, we can reduce the coordinates involved in describing the position of the rigid body to the three Euler angles $\phi$, $\theta$ and $\psi $.
As well as position, we can place constraints on the derivatives of the position coordinates, w.r.t. time, that is the velocities by, for example limiting the CM to move at a uniform velocity, or to rotate in a circle with a uniform angular velocity. In this case we replace algebraic equations by differential equations of motion.
The degree of freedom is the number of coordinates that can vary independently, a holonomic system being one in which the number of independent coordinates is equal to the degrees of freedom of the system. If we need to introduce functions of time, this system is said to be forced, if time is not explicity brought in to the equations, we have what is known as a natural system.
I'd also like if anyone have some mechanical examples, where it gets messy transforming coordinates between different coordinate systems - isn't that the reason it's smarter to use generalized coordinates?
An example in 2 D.

Source: Bead on a Wire - Wikipedia
Assume a bead has the freedom to move along a frictionless wire. The shape of the wire automatically imposes a constraint on the movement in space of the bead. We can rephrase this mechanical constraint in terms of a reaction force C on the bead. Obviously, precisely how we twist and turn the wire in 2 dimensions can lead to elaborate motions of the bead, which may not be easy to mathematically formulate. In the picture above, N represents gravity, which is (the sole) non-constraining force in this 2 D system.
The use of generalised coordinates is based on a careful choice of which of the coordinates should be chosen to be parameterised, if the physical situation allows for this. Thus two variables can be effectively reduced to one when analysing the motion of the bead.
We can express the constraint as $f(r) = 0$, where, at any point in time the position of the bead can be described by $r = (x(s), y(s))$, in this case the arc length $s$ is a parameter, as it is in one of the illustrations at the top of the page.
If we introduce distortions in the path of the bead, that is we bend the wire (within the 2 dimensional space), we end up with an expression:
$${\displaystyle f(\mathbf {r} ,t)=0\,,\quad \mathbf {r} =(x(s,t),y(s,t))}$$
and inevitably t has been introduced, both explicity in the equations regarding constraint and implicitly by means of the coordinates.
Generalised coordinates find their greatest application in Langrangian, and through the appropriate transformation, Hamiltonian systems.



