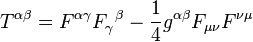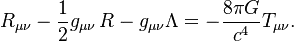How much choice did Einstein have in choosing his GR equations?

Question

General relativity was summarised by Wheeler as "Spacetime tells matter how to move; Matter tells spacetime how to curve". I have a fairly good mental picture of how the first part works.

However, I don't have much of an understanding of the second part. In particular, what I'd like to know is whether the equations describing how matter tells spacetime "could have been different." In other words, did Einstein choose the form of his equations to fit empirical observations, or are they the sort of thing that are worked out entirely from first principles and can't be changed at all without breaking the whole theory?

Evidently there was some choice in choosing the equations, namely the cosmological constant - Einstein included it originally, then took it out, and now it seems like it might be there after all. But is adding a cosmological constant the only possible way in which Einstein's equations can be modified?

Another way to ask this question is to ask what assumptions are required to derive general relativity. I know that deriving special relativity really only requires the principle that the laws of physics (including Maxwell's equations) are the same in all intertial reference frames, and I know that the first part of Wheeler's quote comes from the principle of equivalence between gravity and acceleration. But what, if any, additional assumptions are required in order to determine the way in which matter curves spacetime?

Answer 1

I think Hawking, Ellis "The Large Scale Structure of Space-Time" 3.4 would be an interesting read for you.

From this book:

With Ricciscalar $R$, cosmological constant $\lambda$ and matter Lagrangian $L_m$ $$ I=\int_M (A (R - 2 \lambda ) + L_m) $$

One might ask whether varying an action derived from some other scalar combination of the metric and curvature tensors might not give a reasonable alternative set of equations. However the curvature scalar is the only such scalar linear in second derivatives of the metric tensor; so only in this case can one transform away a surface integral and be left with an equation involving only second derivatives of the metric.

If one tried any other scalar such as $R_{ab}R^{ab}$ or $R_{abcd}R^{abcd}$ one would obtain an equation involving fourth derivatives of the metric tensor. This would seem objectionable, as all other equations of physics are first or second order. If the field equations were fourth order, it would be necessary to specify not only the initial values of the metric and its first derivatives, but also the second and third derivatives, in order to determine the evolution of the metric.

Another nice read is Carroll "Spacetime and Geometry: An Introduction to General Relativity" 4.8. Alternative Theories. There is an shorter version online for free in Chapter 4 here

Answer 2

The empirical restrictions are some obvious ones, e.g. once you have the equations, the earthly results should look Newtonian to some extend, see e.g. this.

Apart from this hand on conparison with experiment, there is of course lots of conceptual work going into the theory, specifically overcoming the problems of Newtonian mechanics per se and then also the unification of special relativity with gravitation. But your question seems to start with the idea of a spacetime metric etc. already in mind.

---

What you certainly like to have are geometric equations, i.e. tensor equations you could write also in index free form. The energy quantity at hand is the classical stress momentum tensor and the theory will hopefull predict its relation $$T_{\mu\nu}=\dots$$ to the space time metric in one way or the other. Start from there, collect all the things you have to put in, these will be the metric, its derivations and maybe simpler (scalar) quantities. The tensor will force the right hand side $$\dots=G_{\mu\nu}$$ to have some properties, e.g. it's a symmetric tensor, it have vanishing divergence due to $\nabla T=0$ and then there are some trace features, and so on. E.g. you see some explicilty for electromagnetic fields.

You always find this awkward form "nice tensor quantity minus some constructed object" if conditions are worked in. I mean the Einstein equations themselve have this kind of form with

or equivalently

In any case it reads $$T\propto G,$$ where one could argue that $T$ is the smallest object you want to express dynamically. Einstein worked the left hand side in this eqauation out. Apperently David Hilbert came up with the theory features parallel with Einstein (there is lots on that "Hilbert-Einstein priority dispute" e.g. here), but he didn't write down the fancy tensor. I mean it's the Einstein tensor after all.

---

Lastly, here is a dizzying list of ideas you might not be familiar with. And these are classical.

I also find it interesting to note that there were theories predating general relatvity

Moreover, apart from these direct (more complicated?) alternative ideas, I've seen some explicit theoretical work of (quantum) approaches "above" general relativity, producing these and that geometrical expressions involving curvature tensors and their product and whatever you can think of. But I guess they will only be talked about once they can be compared with cosmological observations, which need explainations that general relativity doesn't give.