Measuring length in relativity

Question

In Special Relativity I recall the following two definitions:

1. proper length $L_0$: it is the length of an object measured in an inertial frame S in which the object is at rest. In S the endpoints of the object can be measured at different times or simultaneously, both methods yielding (in S) the same result. In all other inertial frames (moving with respect to S) the measured length $L$ is less then $L_0$: $$L = \frac{L_0}\gamma<L_0.$$ I think that I can say that the length, measured where the object is at rest, is the maximum measurable length of the object.

2. proper distance $\sigma$: it is the invariant spacelike interval between two events A and B. If they lay in the x axis of an inertial frame the (square of the) proper distance is: $\sigma ^2=\Delta x^2-c^2\Delta t^2$. Assuming that in S the events A and B are a rest and assuming that they occur at the same time: $$\sigma ^2=\Delta x^2.$$ I think that I can say that $\Delta x$ is the spatial distance measured in S between the two events at rest.

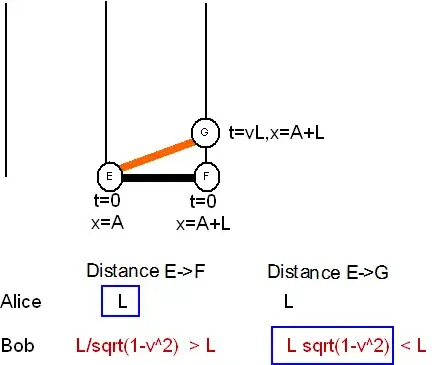
Here my misunderstanding: can I say that in S, where all is at rest, this spatial distance is the length of an object whose endpoints coincide spatially with the two simultaneous events A and B? That is, can I say that: $$L_o=\Delta x?$$

If no, why not?

If yes, since the proper distance for the same two events A and B for the frame S' moving with respect to S along the $x$ axis is $\sigma^2=\Delta x'^2-c^2\Delta t'^2$, from the invariance of $\sigma$ (that is $\Delta x^2=\Delta x'^2-c^2\Delta t'^2$) follows that $\Delta x'^2=\Delta x^2+c^2\Delta t'^2$. But then $\Delta x'>\Delta x$ for every S', so $\Delta x$ (the length, measured where the object -that is, the spatial distance between the two events A and B- is at rest) is the minimum measure of the lenght!

Seemingly, I have two different ways to measure the length (at least when the endpoints of the object can be measured simultaneously), one yielding a maximum, the other yielding a minimum... and I'm a little confused!

I know that I'm doing a mistake, can please somebody help me to find it?

Thank you

er

Answer 1

Always draw a picture!

Here the vertical black line is the observer on the ground and the two thin red lines are the ends of a moving stick.

The coordinate labels are all taken from the frame of the ground observer.

The thick black horizontal line is the stick at a given moment, according to the observer on the ground. Its length, in the ground frame, is $L$.

The thick red line is the stick at a given moment, according to a rider on the stick. The length of the stick, according to that rider, is the Lorentz distance between the two endpoints of that line. Everyone agrees on that Lorentz distance, so you can compute it in the ground coordinate system, and will easily find it to be $L_0=L/\sqrt{1-v^2}$, which is greater than $L$.

The mistake you've been making (which you'd have avoided if you'd drawn the picture!) is to think that there are two events $E$ and $F$ that represent the front and back of the stick at a given moment according to both observers. (I've changed your $A$ and $B$ to $E$ and $F$ because my picture uses $A$ for something different.) But as you can see in the picture, there are THREE relevant events here, not two. The observer on the ground is looking at the distance between the events at the two ends of the thick black line, while the observer on the stick is looking at the events at the two ends of the thick red line. That's three events altogether.

Edited to add: Here's a different picture that I think more closely matches the way you're thinking about this:

(In the other picture, the stick was stationary with respect to the red frame; now it's stationary with respect to the black frame.) Alice is the (black) ground observer and Bob is the (red) moving observer.

The blue boxes show Alice's and Bob's assessment of the length of the stick.
Note that Bob says the spatial distance from $E$ to $F$ (which Alice calls "the length of the stick") is greater than $L$, but he also says that the length of the stick (by which he means the spatial distance from $E$ to $G$) is less than $L$.

Answer 2

Suppose we have a rod of length $\ell$ lying along the $x$ axis in the frame $S$, and at time zero we label the spacetime points marking the ends of the rod $A$ and $B$. So for example $A$ might be the point $(0, -\ell/2)$ and $B$ would be $(0, +\ell/2)$.

In a moving frame $S'$, an observer observes the rod to have a length $\ell/\gamma$ due to the Lorentz contraction, and they label the spacetime points marking the ends of the rod $A'$ and $B'$. So for example $A'$ might be the point $(0, -\ell/(2\gamma))$ and $B$ would be $(0, +\ell/(2\gamma))$.

But ...

The points $A$ and $A'$ are not the same point and the points $B$ and $B'$ are also not the same point. When the observers calculate the length of the rod they are not calculating the distance between the same pairs of points. That is what is throwing your calculation awry.

I go into the reasons for this in detail in my answer to "Reality" of length contraction in SR and I direct you to that question for the details. In brief, for the moving observer one end of the rod is rotated into the future and the other end is rotated into the past. But of course an observer cannot simultaneously see the future and the past - they see where the ends of the rod are at the same coordinate time. That means when the observer in $S'$ sees the ends of the rod they have moved from when the observer in $S$ sees the ends of the rod. It is this movement that causes the rod to be contracted.

Answer 3

Thanks WillO, perhaps I'm a bit dull... I agree with your picture, and that picture is OK with the Lorentz transform (my point 1). But now I think of only two spacelike events E and F in spacetime, as seen by two observers, S and S'. This two events in S have same time coordinate and different space coordinates and (my point 2) I think that the difference in space coordinates is the length of a stick at rest in S whose endpoints in S are coincidental with the space coordinates of E and F.

From this single fact (if it IS right...) via the invariance of the interval for the same two events E and F as seen by S' it appears that the length of the stick for S' is greater that the lenght measured by S, where the stick is at rest... or $\Delta x'^2=\Delta x^2+c^2\Delta t^2$ is perhaps not related to the length of the stick for S'? To reiterate: S' is not measuring a length, S' has only made the math to find the invariant interval between the two events E and F.

Thank you