It's really nice to see someone asking things rather than accepting them without a deeper understanding!
First I'll explain how I think about these operations and then try to answer your questions.
Dot Product:
For me, when you are doing a dot product, you are thinking on how a vector influences in another vector. For example... When you are playing Mario Kart, you have some boosts in the track:
$$
\vec{a} \text{ } \cdot \text{ } \vec{b} = |a||b|\cos(\theta)
$$
Consider the $\vec{a}$ the red vector and $\vec{b}$ the blue vector.
If the angle between them is $0$, you'll see that you are going to get the maximum boost possible, because $\cos(0)=1$. When you start increasing the angle between them, you can see that the dot product is going to approach zero (can you tell why?).
Thinking that way, you can see that the the scalar, that is the result of a dot product, is telling you how much one vector is influencing the other one.
One other thing to build your intuition is to think about how to the computation of a dot product is done:
All images I've got from betterexplained.com, I recommend this site for building up your intuition.
Now, answering your questions:
Here if we multiply projection of A on B (A cos0) with B, finally that product would be in the direction of B?, am I right or wrong?
You are almost right, if you multiply the MAGNITUDE of the projection, with $\vec{b}$ you are going to do a normal scalar-vector multiplication, hence, the result is going to be a multiple of $\vec{b}$ in direction of $\vec{b}$
Secondly please specify the difference between this dot product and ordinary multiplication which I stated above (2x3=6)?
Just check how we compute a dot product and you'll see that there is some kind of relation with the algebraic multiplication you've stated!
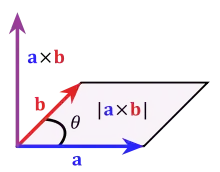
Cross Product:
The result of a cross product:
$$
\vec{a} \text{ } \times \text{ } \vec{b} = \vec{c}
$$
is a vector $\vec{c}$ where this vector is perpendicular to $\vec{a}$ and $\vec{b}$.
When we are looking for computing the MAGNITUDE of the vector in a cross product, you are going to get:
$$
|\vec{a} \text{ } \times \text{ } \vec{b}| = |a||b|\sin(\theta)
$$
and by analysing that equation you can see that the area of the paralellogram made by $\vec{a}$ and $\vec{b}$ is going to be the magnitude of $\vec{c}$. (can you tell why?)
What is the purpose and meaning of this product?
Everytime in a problem when you just want the perpendicular part of a vector in a calculation you'll deal with the cross product. A lot of definitions in physics use cross product... Here's an example:
$$
\vec{f} = q(\vec{v} \text{ } \times \text{ }\vec{b})
$$
That's an equation in electromagnetism that defines what is going to be the force $\vec{f}$ acting on a charge $q$ that is with the velocity $\vec{v}$ in a magnetic field $\vec{b}$.
Why the cross product is always perpendicular to the given vectors?
The reason why the cross product is a vector perpendicular has to do with its computation, that deals with determinant.
I don't know if I should get into in explaining why its vector result is perpendicular because it's not that trivial since its computation deals with determinant, a thing in math that most people use but don't know what it is! If you really want to, comment this post that I'll try to explain!
When I said "can you tell why", I want to see if you are understanding what I'm trying to explain... If you can't figure it out, comment and I'll help you!
Hope it helps!
Keep studying and being curious, but some things are hard to prove without a deeper mathematical approach, and you'll need to handle them by intuition until you get some maturity in math (I'm not that mature in a lot of the situations! hahaha)
