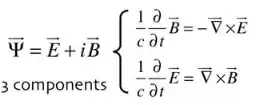4

Sometimes (only when convenient) I hear professors and textbook writers considering the 4-vector potential $A_\mu=(\vec A,\phi)$ as the wave function of a photon. However, since photons have spin 1, I think the wave function of a photon should be a 3-vector.

For example, my professor of subnuclear physics used this argument to justify the fact that photons have parity $-1$: under inversion of parity the verse of currents changes and so does the magnetic field, which means $A_\mu$ becomes $-A_\mu$ under P transformations.

Lello
  • 41
  • 2
    There is no such thing as a wave function for a photon. A photon is the force carrier of the electromagnetic field and is automatically introduced by QFT: in quantum mechanics (or even worse classical electromagnetism) there is no photon. – gented Jun 02 '17 at 11:20
  • 1
    Related/possible duplicate: https://physics.stackexchange.com/q/28616/50583 and its linked questions. – ACuriousMind Jun 02 '17 at 11:21
  • @GennaroTedesco If the discussion is about photons, then we are not talking about semi-classical QM, we are discussing QFT in which case all "particles" are excitations of a field: the electron of the electron field (calculated using Schrodinger's Equation), the photon of the EM field (the harmonic field whose physical shape is determined by Maxwell's equations). So is this issue merely semantics? – garyp Jun 03 '17 at 14:33
  • @garyp Still, there is no "wave function" of the photon (unless by "wave function" you mean something that isn't a wave function). Also, photons emerge as force carriers of the EM field, which is slightly different from excitations. – gented Jun 03 '17 at 19:03

2 Answers2

3

Contrary to a comment, there does exist a wave function for the photon because the quantized Maxell's equation, where the derivatives are interpreted as operators acting on the wave function represents the photon quantum mechanically.

In this link one can see the analogue between electron and photon wave equations;

In modern terms, a photon is an elementary excitation of the quantized electromagnetic field. If it is known a priori that only one such excitation exists, it can be treated as a (quasi) particle, roughly analogous to an electron.

These are in E and B classical fields, but these are connected with the four vector potential, as discussed here.

It should be clear that an individual photon does not have an electric or magnetic field when measured. These reside in the complex valued wave function :

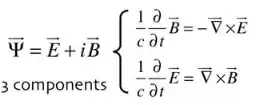
photwv

Note that it is a vector, because of the spin 1 as explained in the link.

It is the superposition of innumerable complex photon wave functions that build up real valued E and B fields of classical electromagnetism. Remember that to get a measurable observable one has to square this superposed huge wave function, so it is not a one to one correspondence from quantum to classical.

How the classical electromagnetic field emerges from a confluence of photons, is shown, using the Quantum Filed Theory formalism in this blog by Motl.

The bottom line is that classical electromagnetism solutions work very well and in courses no emphasis is given to the underlying quantum mechanical wave function. of the photons.

anna v
  • 233,453
  • It's still not clear to me though, what in the above description represents the "wave function of the photon". What would that be? – gented Jun 03 '17 at 19:05
  • @GennaroTedesco The image in the middle IS the wave function of a photon, which will give in a bra and ket notation the expectation value of an observable, as it would for an electron wave function. In QFT it is the photon field on which photon creation and annihilation operators operate. The classical electric and magnetic fields that an ensemble of such photons would generate appear as the components of a plane wave which is assumed to permeate all space for a photon field. – anna v Jun 04 '17 at 02:57
  • So basically you are taking the combination of electric and magnetic field and calling it "wave function of the photon": how so? Moreover, are those classical fields or is this a QFT description? Reading the answer it seems that you are essentially taking the e.m. field and calling its solutions "photons". – gented Jun 04 '17 at 19:42
-1

$A_\mu$ is the solution of equation of motion from Maxwell's Lagrangian. These fields are some time also called "wave solutions" forexample see Mark Burgess Classical Covariant Fields equation 2.49, in momentum space we write $$A_\mu(k)= C_k exp^{ik_\mu x^\mu}.$$

On the other hand the parity transformation you gave is wrong. This is a vector field which transform like a vector under parity transformation. $$A_\mu=(\phi,\vec A)$$ after parity transformation $$A^P_\mu= (\phi,-\vec A).$$

So $$A^P_\mu \not= -A_\mu$$

Zohaib Aarfi
  • 301