3

problem

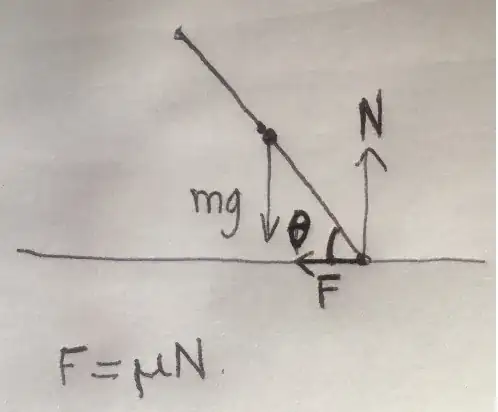
I have a few question about equations of the uniform slender bar motion.

The bar is released from rest on a horizontal surface as shown in the figure and falls to the left. The surface is rough so friction forces are applied at bottom end of the bar. The coefficient of friction is μ and the mass of the bar is 'm'

First, I want to know the angle β when the end of the bottom end of the bar begins to slip. I know that if the x-axis direction force gets bigger than the static friction force it will start to slip. But I can't figure out the equation about the x-axis direction force as function of θ.

Second, I want to know the angle α when the bottom end of the bar starts to lift off the ground. This situation will happen when the normal force is zero. But I can't figure out the equation of the normal force as a function of θ.

I want to know the equation to calculate the alpha and beta.

The problems are not related, it's a different problems.

Any hints or opinion would be appreciated.

Lee
  • 43
  • 1
    This is homework, so ill just give a hint. Before the bar slips you can treat the gravitational potential as being converted to both rotational energy of the bar 1/2Iw^2 and kinetic energy of the center of mass of the bar. You should be able to express this on terms of theta which you can then use in your x-direction force equation – R. Rankin Jun 10 '17 at 07:19
  • Do you know the answer to the question? – Tausif Hossain Jun 10 '17 at 09:05
  • Is it by any chance arctan(1/u) ? – Tausif Hossain Jun 10 '17 at 09:06
  • @R.Rankin So, you mean If the longth is L, T1=0 and V1=(L/2)mgsinθ, T2=(1/2)m[{(L/2)wsinβ }^2+{(L/2)wcosβ }^2]+(1/2)Iw^2, V2=(L/2)mgsinβ. and there's only conservative force then T1+V1=T2+V2. is it right? if θ ans L is given I can calculate the β. and this would be the answer? – Lee Jun 10 '17 at 09:40
  • @TausifHossain Sorry I don't know the answer.. – Lee Jun 10 '17 at 09:40
  • Please show your attempt to answer the question. – sammy gerbil Jun 10 '17 at 14:23
  • @sammy gerbil sorry I'm trying to do my best. – Lee Jun 10 '17 at 15:19
  • Doing your best is not the point. If you do not have any idea how to attempt this question, go back to an easier problem and come to this one later. – sammy gerbil Jun 10 '17 at 15:24

2 Answers2

1

Take this diagram as a hint:

Take torques by considering the center of mass as the pivot. The torque due to friction must equal the torque due to the normal reaction for the rod to not slip.

I think you'll arrive then at the answer for the coefficient of friction.

Mitchell
  • 4,907
Tausif Hossain
  • 2,958
0

Given that the bar is narrow, it would not have to tip very far for the center of mass to be vertically outside the base and therefore topple.

Hint for calculating alpha: consider how fast the top of the bar would have to accelerate in order for the bottom to lift off of the ground, and that it should rotate around the center of mass if this happens.

Hint for mass: the force of friction is equal to μ times R, and f=ma, the acceleration does not depend on mass, only the absolute value for friction will change.

Alex Robinson
  • 1,182
  • But the question is what will be the value of the COEFFICIENT of friction for not slipping, not the acceleration or velocity. – Tausif Hossain Jun 10 '17 at 09:44
  • @TausifHossain my bad, i will edit my answer – Alex Robinson Jun 10 '17 at 09:46
  • @Cursed1701 question is what will be the angle α, β – Lee Jun 10 '17 at 10:24
  • @Lee i reccomend you read the help center, in particular the site policy on "homework style questions", we cannot give you a full worked solution, only hints and answers to questions about understanding, I have given information which ought to be useful in determining alpha and beta – Alex Robinson Jun 10 '17 at 10:25
  • @Cursed1701 I thought you edit your answer for the coefficient of friction. The coefficient of friction will be given so It's not important to get it. – Lee Jun 10 '17 at 10:41