I highly recommend the first chapter of the book Quantum Physics of atoms, molecules, solids, nuclei and particles by Eisberg & Resnick.
It's an easy read and it's explanation of energy quanta is unparalleled. But I will still try to explain as briefly as possible.
Now classically, a large system of non interacting entities are assumed to follow Boltzmann distribution which allots the probability of an entity possessing an energy in any range. Now combining this with the freedom of all possible continuous energies gives the average total energy to be $kT$ for each entity.
In the case of black body radiation the entities are the standing waves with fixed wavelength satisfying the condition that they must have nodes at the walls of a black body. Since we allotted the same average total energy to each mode of standing waves and the possibility that every mode can combine to give the total power spectrum, we give rise to divergences at large frequencies as the number of modes can just keep on increasing. This is called the Ultraviolet Catastrophe of the Rayleigh-Jeans formula.
Now experimentally the Rayleigh-Jeans formula suited well at low frequencies but not at higher frequencies . Whereas the power spectrum should go to 0 at higher frequencies, Rayleigh-Jeans formula gave infinities. So to get rid of this problem, the average total energy of the modes should go to 0 at large frequencies and $kT$ at small frequencies.
There are two ways of fiddling with the average total energy for each mode.
1) Either change the distribution law from Boltzmann's to anything else or
2) Change the classical assumption that each mode gets equal average total energy $kT$.
Now Planck was not aesthetically inclined to do the former as that distribution law explained many other phenomena splendidly. So he did the latter. He tried to guess the function by noting that instead of assuming continuous range of energies if he assumes that energy could only take values that are the multiples of a quantity(the minimum possible energy, say $E_o$) then he could get such a desired function.
Now the distribution law is:

a) if we assume $E_o\ll kT$, then average energy $E_{avg}\sim kT$

b) if we assume $E_o\sim kT$, then average energy $E_{avg}\lt kT$

c) if we assume $E_o\gg kT$, then average energy $E_{avg}\ll kT$

Recapitulating, Planck discovered that he could obtain $E_{avg}\sim kT$ when the difference in adjacent energies $E_o$ is small, and $E_{avg}\sim0$ when $E_o$ is large. Since he needed to
obtain the first result for small values of the frequency and the second result for large values of frequencies, he clearly needed to make $E_o$ an increasing function of frequencies. Numerical work showed him that he could take the simplest possible relation between $E_o$ and frequency having this property. That is, he assumed these quantities to be proportional. Adding a proportional constant he postulated:
$$E_o=h\nu$$
where $h$ is the proportionality constant (called Planck's constant) and $\nu$ is the frequency.
Using this formula for allowed energies we get the average energy for each mode as:
$$ \bar{\mathscr E} = \frac{h\nu}{e^{h\nu / kT} - 1} $$
and the power spectra as:
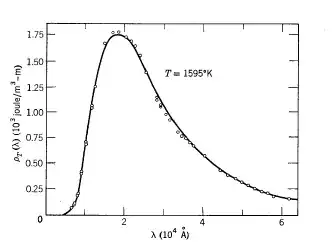
$$ \rho_T(\nu)d\nu = \frac{8\pi\nu^2}{c^3} \frac{h\nu}{e^{h\nu / kT} - 1}d\nu $$
which fits with experiments phenomenally well: