Is it normal for physical functions to lack a 2nd derivative?

Question

My question is about the appearance of a non-analytic function in the formula for the resistive force in air or other medium. Considering the 1-dimensional case as covered by Walter Lewin in his 8.01 lecture, the magnitude of the resistive force is proportional to the square of the speed of the object, which we take to be a sphere. In other words

$$|F|=cv^2$$ with the force being in the opposite direction of the object's motion.

The constant $c$ depends on the sphere's radius, drag coefficient of air and so forth, but for convenience choose values that make $c=1$.

I understand this is an approximation, and in reality there is a $v$ term as well as the $v^2$ term, and maybe other terms as well, but I don't think that invalidates my question.

With that said, here's is a graph of the resistive force $F$ as a function of $v$:

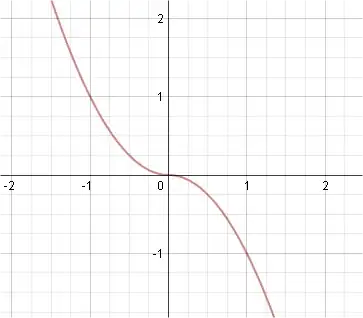
Because the sign of the force is opposite that of velocity, the equation can be conveniently written $$F=-v|v|$$

Although this function looks smooth and has a derivative, $2|x|$, it doesn't have a second derivative. Isn't it unusual for a simple equation of a physical phenomenon in classical mechanics to lack a second derivative? It's unintuitive to me that the force doesn't have a second derivative. Physically, it doesn't feel like anything non-smooth is going on.

My question: Is it normal to encounter functions in classical mechanics with no second derivative, and if not, what's the explanation for finding one here?

Added: For anyone interested in this topic, a related question popped up over at MathOverflow and there are several good answers.

Answer 1

That function actually does have a well-defined second derivative at every point except $v=0$, which is a perfectly reasonable thing to have happen in physics. It's often the case that different domains of a system have different behavior, and in a continuous approximation, these domains have sharp boundaries, which can lead to second (or even first) derivatives which are not well defined at isolated points.

This isn't normally an issue because we only ever deal with approximate measurements in physics. You may be familiar with the idea that it's impossible for a measurement to produce an exact rational value; this is basically the same idea. The behavior of a function at a single isolated point (or any set of points of measure zero, I think) is irrelevant because you're never going to sample the value at that exact mathematical point in practice.

If you were talking about a function whose second derivative was not defined anywhere, that would be a different matter entirely. We don't usually deal with those sorts of functions in physics.

Answer 2

As David says, smoothness is a very subtle thing.

There are "analytic functions" which have all derivatives and in fact, they are equal to their Taylor expansion everywhere in a vicinity of any point. Those functions are very natural in complex calculus and physics, too. Every function that ever appears in physics may be at least "approximated" by analytic functions arbitrarily accurately. In this sense, the analytic and "totally smooth" functions are enough.

However, physics also allows us to work directly with functions that are not smooth because they're sometimes natural and needed. For example, your function $$ F(v) = -v |v| $$ may be differentiated everywhere using a formalism of distributions that Paul Dirac introduced into physics (and mathematics) and that became very important in physics. The first derivative is $$ F'(v) = -2v \cdot \epsilon(v) $$ where the epsilon funtion is the sign function. However, what's funny is that we may give a compact formula for the derivative of $F'$ i.e. second derivative of $F$, too. It is: $$ F''(v) = -2\epsilon(v) - 4v \delta(v) $$ where I used that the derivative of $\epsilon$ is twice the derivative of the ordinary step function $\theta(v)$ and the latter is nothing else than the Dirac delta-function. This form of $F''(v)$ knows about the unsmoothness at $v=0$ and allows us to be integrated again to return back to $F'$ and then to $F$ (plus minus an integration constant).

When you look into the modern physics literature, you will find delta-functions and their derivatives almost everywhere which also means that you may find step functions (or epsilon) and functions such as $-v|v|$ that are not completely smooth (infinitely differentiable or analytic).

To a large extent, you may require all functions in physics to be infinitely smooth and you won't really lose anything. However, it's often more convenient to allow unsmooth and even discontinuous functions (and their derivatives that include delta-functions etc.) and work with them directly. Physicists know how to do it efficiently. That's e.g. what continuous bases in quantum mechanics or Green's functions are all about.

There are various universal physics conditions such as the normalizability of wave functions or the finiteness of energy that constrain the allowed forms of the functions that appear in fields or wave functions etc. For specific conditions, one may reformulate them in equivalent ways. However, the universal big question "Should we allow unsmooth functions in physics" doesn't really have a universal objective answer. It's often up to the taste of a particular physicist. Most physicists usually don't care about such things too much. If you develop an axiomatic framework for fields or wave functions etc., you must decide how much unsmooth or pathological functions you allow. But those choices won't really change the "physical content" of the theories because unsmooth functions may always be arbitrarily closely approximated by smooth ones and vice versa.