1

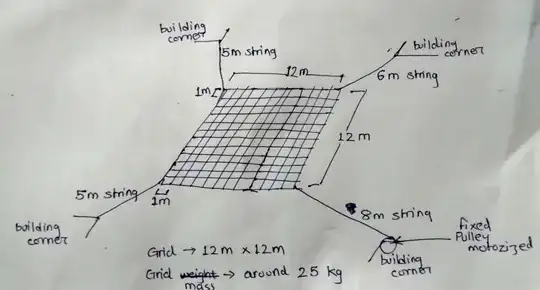
I am a software developer and helping someone with an art installation. It consists of a grid made of ropes.

Grid is $12 \cdot 12$ meter and internal squares are $1 \cdot 1$ meter. Grid is suspended in air (at height of around 7 meter) by strings tied to each one of its four corners.

Three of the four strings are around 5 meter, 5 meter and 6 meter in length, but the fourth one is around 8 meter. I can measure the distances (in $x$ and $y$ components) from each of the corners to the point (on building/ structure) where they are tied. This would help in calculating theta angle, right?

I have searched over the web and found resources to calculate tension in strings. But all of them show how to calculate tension for an object suspended by two strings at a common point.

I need to calculate tension exerted by strings tied at different points of object (each one of four corners.)

Please correct me anywhere I am going wrong. Also, any pointers would be appreciated.

EDIT : One of the corners, the one tied with 8 meter long string would be tied to a motorized pulley for winding/unwinding.

enter image description here

Qmechanic
  • 201,751
Chandan Pednekar
  • 11
  • A diagram would be nice. – Zhengqun Koo Dec 08 '17 at 15:36
  • 1
    Added diagram.. – Chandan Pednekar Dec 10 '17 at 17:02
  • Just curious; what is the motorized pulley supposed to do here? If you're using that to move something while this is installed, this is no longer static and that would change the results. – JMac Dec 29 '17 at 12:47
  • This question is better suited for [Engineering.SE]. Also, not enough information is given as the amount of droop (or angles) affects the tensions, and the height of the support points may vary changing the geometry. Best answers would come from some sort of simulation, rather than static theory as the weight and elasticity of the ropes may play a role here. – John Alexiou Dec 29 '17 at 13:10

1 Answers1

1

Assuming that the structure is in static equilibrium (ie it is not accelerating in any direction, neither is it accelerating rotationally) then the usual conditions apply :

  1. the resultant of forces on the structure must be zero
  2. the resultant moment of forces must also be zero.

If you apply these 2 rules to the forces acting on the grid you can find the unknown tensions in 3 of the 4 strings. The weight of the grid is a 5th force acting vertically down on the centre of the grid. I assume that you are given the positions of the points to which the ropes are attached. Geometry will tell you the angle each rope makes with the horizontal. Then you only need to find the 4 tensions.

Condition 1 enables you to write 2 equations, for the vertical and horizontal directions. Condition 2 enables you to write another 1 equation. So you can find a maximum of 3 unknown forces using these conditions alone.

If you can measure the tension provided by the motor, then you can find the other 3 tensions. Otherwise the rigid body model cannot provide a solution : see A simple (?) problem of static equilibrium. You would have to introduce some other information such as the elasticity of the strings.

sammy gerbil
  • 27,277