1

I realize that there is a lot of topic's mentioning this, but I think my question is rather new compared to many of them.

First of all, this is part of a school assignment, and our object is to replicate Young's double slit experiment. I am familiar that the original experiment isnt a double slit, but to get familiar with the basics, I will start with the double slit.

The question is, how does the interference pattern depend on x, dx and lambda? Where is x is the distance between the slits, dx is the width of the slits and lambda the wavelength. Most of the answers I've found connects the interference pattern with x and lambda, but simply leaves out dx since it's supposed to be so "very small".

My project requires me to find a lot of information, so if anyone knows a good source of finding information in the subject, please let me know.

Qmechanic
  • 201,751
John Skeet
  • 131
  • $dx$ is usually not important because the usual approximation is to consider the slits 1D sources (i.e., lines, or, in the typical side view of the experiment, point sources). – stafusa Jan 28 '18 at 14:40
  • I will be trying to replicate the experiment myself, so I think the usual approximation by considering 1D sources isnt avaible anymore for me.

    I'm trying to find some sort of connection between x, dx and lambda, but as you mention, the connection between two of them are easy to find, but to include dx seems harder. Am I searching in vain for this connection?

     – John Skeet Jan 28 '18 at 14:50
  • I'm no specialist, but I understand that as long as $dx<\lambda$ that's a pretty good approximation, isn't it? If you're not in this regime, than you should properly take diffraction into account. I think you can find some answers googling for Young's experiment with finite slit width. E.g., https://phys.libretexts.org/TextMaps/General_Physics_TextMaps/Map%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_III_(OpenStax)/4%3A_Diffraction/4.3%3A_Double-Slit_Diffraction or http://web.mit.edu/viz/EM/visualizations/coursenotes/modules/guide14.pdf – stafusa Jan 28 '18 at 15:02

1 Answers1

10

A double slit arrangement with each of the widths of the slits being very, very small produces this interference pattern.
It is a graph of relative intensity (y-axis) against position (x-axis).

enter image description here

A single slit of finite width produces a diffraction pattern.

enter image description here

Now if you have a double slit arrangement with slits of the width that produced the diffraction pattern above you get the following interference pattern.

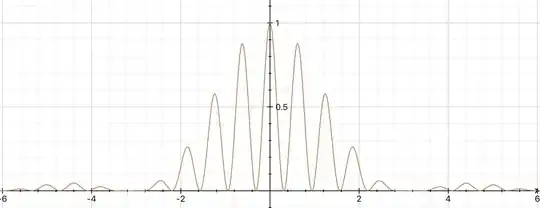
enter image description here

You will note that the single slit diffraction pattern controlled by the width of the slits modulates the intensity of the double slit interference pattern.

Here is the sort of pattern that you might observe on a screen:

enter image description here

Now if the slit width is halved then the diffraction pattern due to a single slit of that width looks like this.

enter image description here

The diffraction pattern is wider than the single slit diffraction pattern shown before.

Using two slits of this width whilst keeping the slit separation (centre to centre) the same as before results in this interference pattern.

enter image description here

So you will note that the slit widths control the modulation of the intensity of the double slit interference pattern.
The slit separation controls the separation of the interference fringes.
As the slit separation has not been changes the separation of the interference fringes stay the same.

So the very first diagram is an interference pattern with two slits which are very narrow and hence produce a very broad diffraction pattern.

Update as a result of a comment.

The third graph was produced using

$$y = \left (\dfrac{\sin\alpha}{\alpha} \right )^2 \cdot \cos^2(5 \alpha) $$.

The first term is the diffraction envelope and the second term the interference fringes.

There is more about how the angle $\alpha$ is related to the wavelength of the light, the slit width and the slit separation in this answer and in many textbooks and websites.

Farcher
  • 95,680