To solve this, we can simply go through the derivation of the Carnot efficiency, taking account of the possibility that $T_H$ might be negative. For some reason I can never think about heat engines without drawing a diagram. Here's a diagram of how a normal heat engine works, using reservoirs with positive temperatures:

Fig. 1: A normal heat engine.
The engine takes an amount of heat $Q_\text{in}$ from a reservoir at temperature $T_H$, and outputs an amount of work $W$, as well as rejecting an amount of heat $Q_\text{out}$ into a reservoir at temperature $T_C$.
The first law says that $Q_\text{in} = W + Q_\text{out}$. The second law says that the total amount of entropy must increase. The entropy of the hot reservoir drops by $\frac{1}{T_H}Q_\text{in}$ and the entropy of the cold reservoir increases by $\frac{1}{T_C}Q_\text{out}$. (The work $W$ doesn't affect the total entropy. Work is energy without any entropy).
So the total entropy change is $\frac{1}{T_C}Q_\text{out} - \frac{1}{T_H}Q_\text{in}$, or $\frac{1}{T_C}(Q_\text{in}-W) - \frac{1}{T_H}Q_\text{in}$. The efficiency is maximised when this is set to zero, which leads to the Carnot efficiency
$W_\text{max} = \left( 1- \frac{T_C}{T_H}\right) Q_\text{in}.$
Now let's imagine that $T_H$ is negative, and see how this picture changes.
The first thing to note is that now, when we remove heat from the hot reservoir its entropy still changes by $-\frac{1}{T_H}Q_\text{in}$. But this is now a positive change, because of the negative sign of $T_H$. You can think of $\frac{1}{T} = \frac{\partial S}{\partial U}$ as the amount by which a system's entropy changes when a small amount of heat is added. Energy stored in a negative-temperature reservoir "wants" to become heat, in the sense that removing heat increases its entropy rather than decreasing it.
Now, we can still go through exactly the same reasoning as before, and we still get
$W_\text{max} = \left( 1- \frac{T_C}{T_H}\right) Q_\text{in},$
and as you point out, this will be greater than 1. But note that in this case, $Q_\text{out} = Q_\text{in}-W_\text{out} < 0$. In your example where $\eta=2$, we have $Q_\text{out} = -Q_\text{in}$.
In Kostya's answer it is assumed that $Q_\text{out}$ must be positive, which is why he or she concludes that an engine with this efficiency can't exist. But I want to take a different approach by taking it at face value: the most efficient engine in this situation is one that actually takes heat out of the cold reservoir:
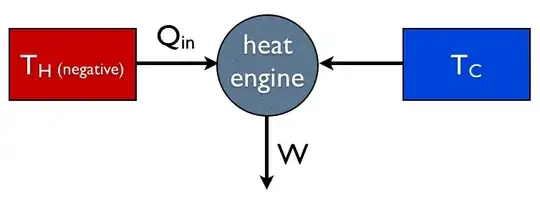
Fig. 2: A super-efficient heat engine, operating with a negative-temperature reservoir. Note that it takes heat out of both reservoirs.
Now we can make a certain amount of sense of the efficiency being greater than one. If $\eta>1$ it means that $W$ is greater than $Q_\text{in}$. But that's ok because in this situation some of the energy is coming from the cold reservoir. There's no problem with the second law, because we derived this by explicitly setting the entropy increase to 0.
I want to go back and make something clear that I hinted at earlier: you can take heat out of a negative-temperature reservoir and turn it directly into work, contrary to the Kelvin statement. That is, this engine is possible:

Fig. 3: A heat engine that converts negative-temperature heat directly into work.
But this does not contradict the second law. The above engine is not maximally efficient and produces an amount $-\frac{1}{T}Q$ of entropy, which again is positive because $T$ is negative.
You can't use it to build a perpetual motion machine, because the temperature of the negative temperature reservoir will decrease as heat is removed from it, until its temperature reaches minus infinity (which it will do in finite time), at which point it will switch to being positive and continue to decrease. This probably sounds pretty counterintuitive, so see the section on it below.
So the upshot of all this is that yes, it's possible for $\eta$ to be greater than 1 if $T_H<0$, but this isn't a counterexample to the second law and doesn't allow the construction of a perpetuum mobile. The Kelvin statement was written before knowledge of negative temperatures, as you say, and to make it true for such systems it would have to be modified to "no process is possible in which the sole result is the absorption of heat from a reservoir with positive temperature and its complete conversion into work."
Why does the temperature decrease to $-\infty$ and then become positive?
In a previous version of this answer I said that you can't create a perpetuum mobile because you need work to create a negative temperature reservoir. This is kind of true, but I think the below is a better argument.
We start by noting that
$$\frac{1}{T} = \frac{\partial S}{\partial U},$$
where $U$ is the internal energy of a system and $S$ is its entropy. For most systems the curve $S(U)$ looks something like this:

Fig. 4: The $S(U)$ curve for a typical object with a finite heat capacity.
You can see that as you remove heat from the system (decreasing $U$), the slope $1/T$ increases (i.e. $T$ decreases) until at some point with finite $U$ (the ground state energy), the entropy becomes zero and the slope becomes infinite (or $T$ becomes zero). It's a basic result from statistical mechanics that the curve $S(U)$ must be concave, meaning that $1/T$ must always be non-increasing with increasing $U$. Typically, $S$ and $U$ are both unbounded.
However, for some systems (those where you can have a population inversion) can only hold a finite amount of energy, and for those systems the curve looks more like this:

Fig. 4: The $S(U)$ curve for a system that can have a negative temperature.
You can see that these systems can have negative temperatures, meaning that the internal energy $U$ is to the right of the peak in $S$. As you remove heat from such a system, $1/T$ increases until it passes through zero and becomes positive again, which corresponds to $T$ decreasing $-\infty$, then swtiching to $+\infty$ and continuing to decrease.
So as you remove energy from a negative-temperature reservoir you're inevitably moving it closer to becoming a normal positive-temperature reservoir. This is the fundamental reason why you can't build a perpetual motion machine using negative temperature reservoirs: eventually the constant-temperature idealisation has to break down, and your negative-temperature reservoir will become a postive-temperature one.
Conversely, in order to create the negative-temperature reservoir in the first place, you'd have to put energy into it. A system with a humped $S(U)$ curve as shown in Fig. 4 will typically start out at the same (positive) temperature as its surroundings, meaning that its internal energy $U$ will be to the left of the peak in the $S$ curve. To make the temperature negative you would have to put energy into it using a heat pump (similar to Fig. 2 but with all the arrows pointing in opposite directions). Essentially, you have to heat it up so much that its temperature becomes infinite, and then negative. So while it might seem quite miraculous that negative-temperature heat can be converted 100% into work without generating any heat, you have to bear in mind that negative temperature systems are something very special that don't (as far as I know) exist in nature, and you can't create one without using up at least as much work as you could extract from it using a heat engine.
Shouldn't heat flow from the negative-temperature reservoir $H$ into the postive-temperature one $C$?
If we were not using a heat engine to extract work then yes, it would. As you can hopefully see quite clearly from Fig. 5 above, negative temperatures are hotter than positive ones. But the point is that we're not just considering a spontaneous flow of heat, we're considering the most efficient way to extract work from the reservoirs, using a hypothetical machine.
It might help to look again at Fig. 1, showing a normal heat engine. Here we have heat flowing out of a hot reservoir, and into a cold one. But the heat going into the cold reservoir is less than the heat coming out of the hot one, because some of it gets converted to work. If we increase $T_H$ while keeping $Q_\text{in}$ constant then the engine can operate more efficiently, so $Q_\text{out}$ will decrease. If we make $T_H$ infinite (i.e. $1/T_H=0$, so the hot reservoir is right at the peak of the $S(U)$ curve above) then $Q_\text{out}$ becomes zero, because the maximally efficient heat engine has efficiency 1 and can convert heat at $T_\infty$ to work without producing any heat. (In a sense, work is heat with infinite temperature.)
If we increase the energy of the hot reservoir even further, so that its temperature becomes negative (passing the peak on the $S(U)$ curve), the maximum possible efficiency becomes greater than 1, and $Q_\text{out}$ becomes negative. Note that in this case the heat engine is removing heat from both reservoirs.




