4

All the SI derived units I know are defined as products of SI units raised to an integer power (e.g. the coulomb is measured in $\text{s}\cdot\text{A}$, the pascal in $\text{kg}\cdot\text{m}^{-1}\cdot\text{s}^{-2}$, etc.).

But are there any meaningful physical quantities for which it makes sense to consider different operations, such as n-th roots, logarithms or exponentials of SI units (things like $\text{m}\cdot\sqrt{\text{s}}$, or $\ln{\text{kg}}\cdot e^{2\cdot\text{cd}}$)? Or trigonometric functions, or even more exotic operations?

And if not, is there a specific reason why there aren't/there can't be any?

Labba
  • 487
  • 1
  • 5
  • 11
  • Related: https://physics.stackexchange.com/q/364771/2451 and links therein. – Qmechanic Feb 16 '18 at 15:48
  • Consider something that is taking a random walk. The standard deviation of position would grow as the square root of time, so the units of its rate of growth would be length / sqrt(time). – Bert Barrois Feb 16 '18 at 16:14
  • 1
    You've asked about SI in particular, but the case of charge units in cgs is worth investigating. – dmckee --- ex-moderator kitten Feb 16 '18 at 17:20
  • The bel or decibel is a logarithmic value. However, it's the logarithm of a ratio relative to some arbitrary reference sound level, so it's not really "composed" of other units. – Hot Licks Feb 16 '18 at 17:25

3 Answers3

5

There's a fair few physically meaningful quantities whose units include half-integer exponent, typically in examples where the quantity in question needs to square to some kind of intensity or density.

  • The clearest one is quantum mechanical wavefunctions $\psi$, for which the square modulus $|\psi|^2$ is a probability density (i.e. with units of inverse length in 1D or inverse volume in 3D) so you'll have $[\psi(x)]=[L^{-1/2}]$ in 1D and $[\psi(\mathbf r)]=[L^{-3/2}]$ in 3D.

  • You very often see the unit $\mathrm{Hz}^{-1/2}$ in any field that requires signal analysis in any capacity, where it comes out naturally as a way to describe amplitude spectral densities of many kinds. This happens when you have some signal $f(t)$ (in, say, dimensionless strain) and you care about its Fourier transform, i.e. you want to represent $f(t) = \int_{-\infty}^\infty \tilde f(\omega) e^{-i\omega t} \mathrm d\omega$ in such a way that $\int_{\omega_1}^{\omega_2} |\tilde f(\omega)|^2 \mathrm d\omega$ represents the power the signal carries in that spectral band.

    A nice, recent example of this in action is the noise sensitivity curves for LIGO and other gravitational-wave detectors as a function of frequency:

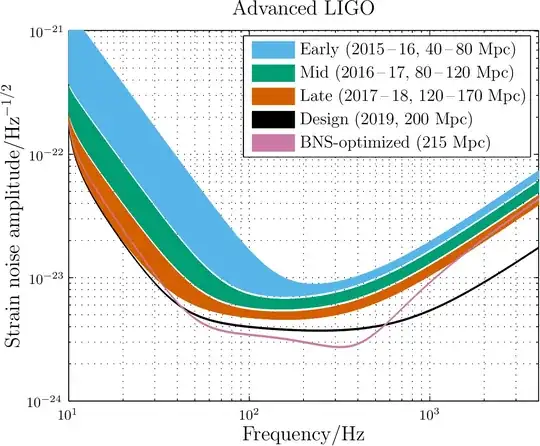
    Image source

If you want to go beyond half-integer powers into proper $n$th roots, then in principle there's nothing to stop you, but the chances of finding physically-meaningful examples do decrease dramatically, because physics tends to use quadratic forms of its dynamical variables far more often than you see cubic or other multi-linear dependences. I'm not aware of any real-world examples, but they're perfectly possible.

Things do change, however, if you move away from rational functions (i.e. combinations of fractional powers) and into transcendental functions (like the exponential, logarithm, and trigonometric functions), which can only be defined meaningfully using processes that add or compare a quantity $x$ with a power $x^n$ of that same quantity. As I explained in this previous thread, this completely breaks dimensional analysis, and it is not meaningful to put dimensionful quantities as the arguments of transcendental functions.

(There is a minor, partial exception with the specific case of the logarithm, where you can "split" a logarithm of the form $\log(q_1/q_2)$ into a subtraction $\log(q_1)-\log(q_2)$ under the strict requirement that all appearances of $\log(q)$ be followed by a corresponding ${-}\log(q')$ with $[q']=[q]$, and that both occurrences take the logarithm of the numerical value in the same units. This is useful if you only care about things up to an additive (or multiplicative) constant, but ultimately it just boils down to an elaborate formalism for dealing with $\log(q_1/q_2)$, i.e. the logarithm of a dimensionless quantity, in a way that allows you to forget that fact.)

Emilio Pisanty
  • 132,859
  • 33
  • 351
  • 666
  • 2
    Not sure whether the wave function is a good example for a "meaningful physical quantity", since it is not observable in itself. – user1583209 Feb 16 '18 at 17:18
  • 1
    @user1583209 Yes it is (as a qualified statement, obviously). If you have a preparation procedure that will reliably produce particles in a pure state with wavefunction $\psi(x)$, then it is perfectly possible to design a procedure that will completely reconstruct $\psi(x)$ all the way up to its minor natural ambiguities (i.e. global phase). – Emilio Pisanty Feb 16 '18 at 17:22
2

Edit: The answer below is certainly suspect. Do read the comments underneath it, and follow the link provided by dmckee.

It doesn't make sense to consider the sine, log or exponential function of a unit or anything with units. One way to see this is to note that these functions can all be expanded as Taylor series. For example,$$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}…$$ It clearly doesn't make sense to try and add a unit (or a quantity with units) to the same unit squared and so on. In more formal language, we would have a dimensional inhomogeneity!

Philip Wood
  • 35,641
  • This is not quite right, since it claims to rule out logs of dimensionful quantities, but logs of dimensionful quantities do make sense. –  Feb 16 '18 at 15:54
  • 2
    @BenCrowell This answer is correct. Logarithms of dimensionful quantities do not make sense: if you're careful, you can compute the difference of the logarithms of dimensionful quantities and produce correct calculations that look like you're using the logarithm of a dimensionful quantity, but ultimately you're just calculating the logarithm of the ratio of those two quantities (itself a dimensionless number). – Emilio Pisanty Feb 16 '18 at 17:00
  • I don't doubt that you're right and I'm wrong, but how do you escape dimensional inhomogeneity as per my argument? – Philip Wood Feb 16 '18 at 17:00
  • Phillip, I have a hugely upvoted answer that follows exactly this argument, and after I wrote it (and it was accepted) I found an interesting comment/counter-argument which is linked therein (and a un-paywalled link in the comments). Lots of discussion about what the Matta paper does or does-not prove in the comments, too. – dmckee --- ex-moderator kitten Feb 16 '18 at 17:24
  • Very nice. Thank you. What do you think of Roan's answer, the one underneath your hugely up voted answer? – Philip Wood Feb 16 '18 at 17:59
  • Philip, I confess I hadn't look at it yet. I want to think about it for a while, but I think that it is a very relevant comment. If it is as compelling as it appears at first glance then it makes the series argument correct and the fun question because "Why does Matta's construction have the right term-by-term dimensions even when the starting place isn't valid?". – dmckee --- ex-moderator kitten Feb 17 '18 at 02:25
1

It does not normally make sense to put anything but a unitless input into a transcendental function. However, as discussed in this question, it does make sense to take logs of quantities that have units. The result is that you get an additive constant that would depend on the choice of units, and this constant is often of no interest. The classic example would be using the slope of a log-log plot to find the exponent in a power law. However, the units of the input are not passed through to the output. So for example, if you take the log base 10 of 100 kg, you get 2 plus a constant, but the 2 doesn't have units of log-kilograms. The choice of kilograms is present in the additive constant. Therefore there is no such thing as a unit of "log-kilograms."

Roots are used in units all the time. For example, I teach a lab in which we drop balls from unequal heights $h_1$ and $h_2$ and measure the time between the two hits in order to measure $g$ with pretty good precision. The expression for $g$ involves the quantity $\sqrt{h_1}-\sqrt{h_2}$.

  • Don't we divide a quantity by its unit before taking the log? Hence we label graph axes "ln($x/$m)" and so on. – Philip Wood Feb 16 '18 at 15:54
  • 1
    @PhilipWood: You can do it that way, but it's a matter of taste. The linked question has some very detailed discussion of this. –  Feb 16 '18 at 15:55
  • @BenCrowell The linked question has a detailed explanation of why your procedure does boil down to dividing the quantity by its unit, as Philip suggests. You might go off and use a formalism that obfuscates that fact, but there's no other way to assign a meaning to $\log(1:\mathrm m)$. – Emilio Pisanty Feb 16 '18 at 17:04