1

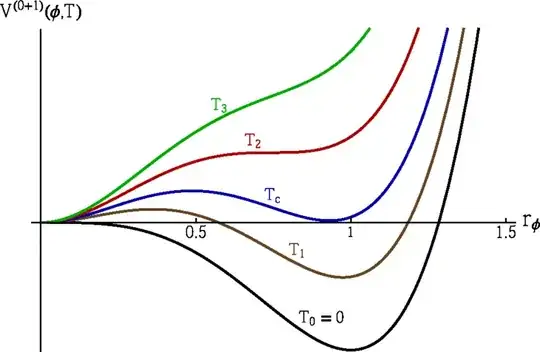
I'm trying to piece together a coherent understanding of the EW symmetry breaking and its effect on early cosmology, from a number of somewhat incomplete sources. Any corrections to the following presumed steps or conclusion would be greatly appreciated. i) In the early universe, before freeze-out, the Higgs field energy was way up on the sides of its "sombrero" potential curve (very high energy level.) ii) Therefore no vacuum expectation value for the Higgs field iii) Thus no EW symmetry breaking iv) All the SU(2)XU(1) symmetric intermediate vector bosons (B and original W) were massless, weak mixing angle = 0 v) Thus the EW force was long range during this time (Until the Higgs field energy falls far enough to acquire the VEV and break the symmetry.) vi) Fermions massless

That seems to me to require a huge recomputation of most SM results and "constants" that would be very different from what we see in experiment today. Little or none of today's data and theory could be applied to that period. Do calculations in cosmology for this period account for this? Is there something missing or wrong in this line of reasoning?

Jim Eshelman
  • 417

1 Answers1

2

Actually, the Higgs has no vev at sufficiently high energies. This is a phoneomenon called symmetry restoration: the Higgs potential receives corrections from the thermal bath, leading to the so-called finite temperature effective potential. The key piece is the effective mass $$m_{eff}^2(T) = -\frac{m_H^2}{2} + cg^2T^2$$ Notice that for $T \gg m_H/g$, a potential of the form $V(\phi,T) = m_{eff}^2\phi^2 + \lambda \phi^4$ will have only a single global minimum at the origin. Here's a schematic of what the potential looks like as the temperature drops:

enter image description here

Notice how the vev only develops after the temperature drops below the critical value.

(figure credit https://www.researchgate.net/publication/264826386_Strongly_First-Order_Electroweak_Phase_Transition_and_Classical_Scale_Invariance)

bapowell
  • 1,762
  • Yes, that's it exactly, the lack of symmetry breaking at high field energies implies a long range EW force (massless intermediate vector bosons) during the first few picoseconds or so of the universe. So the question is how/whether this has been taken into account in calculations for that period such as baryogenesis? Seems like it would require quite a recalculation of many results used in our low energy/temp realm today. – Jim Eshelman Mar 18 '18 at 12:52
  • Yes, it’s taken into account. The temperature-corrected quantities are used so that symmetries are all restored above their critical temperatures. – bapowell Mar 18 '18 at 15:42