Is my understanding of time dilation correct?

Question

Let's say that a spaceship moves with speed $v$ relative to an observer in earth. Let's make the calculations for the reference system of earth, so the observer is stationary and the spaceship is moving with a speed close to the speed of light.

The proper time $\tau$ is the time the stationary observer in earth counts. But the clock in the spaceship is moving slower, so for the spaceship clock, time $t$ will have passed. And this $t$ will be less than $τ$ since the clock is ticking slower inside the spaceship, from the perspective of the unmoving observer. And to find out how smaller it is we need the Lorentz factor: $$t = τ\sqrt{1 - \frac{v^2}{c^2}}$$ which tells us that indeed, $t<τ$.

That's my understanding, but I'm not sure if what I just typed is correct. If someone can tell me if I'm right or if not, or if not what's my mistake then I'd greatly appreciate it.

Answer 1

The formula is correct but use it carefully.

You can't really say "the time is..." on its own. It's all about events. You have to say "Between these two events, the time is ..."

Our use of "proper" in relativity is a bit odd. It does not mean 'good, OK, correct' but means 'belonging to', like in 'property'. The 'proper time' between two events is the time as measured in a frame in which the events occur at the same place - typically ticks of a clock in a frame in which the clock is stationary.

Answer 2

You need to be careful about defining exactly what you mean by time dilation because the term tends to be bandied about with little care for its meaning.

Suppose you have two events in spacetime that two observers can both agree on. For example if we launch a spaceship at speed $v$ towards Alpha Centauri then the two events might be (1) the spaceship leaving Earth and (2) the spaceship arriving at Alpha Centauri. Then time dilation means that an observer on Earth and an observer on the spaceship will measure different elapsed times between the two events. The equation you give relates those two elapsed times.

We tend to call the time measured by the moving observer's clock the proper time, and we give this the symbol $\tau$. The time measured by the observer on Earth is called the coordinate time and generally given the symbol $t$. Then we have the relationship:

$$ \frac{\tau}{t} = \sqrt{1 - \frac{v^2}{c^2}} \tag{1} $$

That is, the time measured on the spaceship $\tau$ is less than the time measured on Earth $t$.

But be careful about casually applying this formula because it applies only in some circumstances. Using the formula without thinking in your physics exams is an excellent way of failing them. If you're interested in finding out more about what time dilation means then see What is time dilation really?

Response to comment:

In special relativity the proper time $\tau$ for a trajectory between two points is defined by the Minkowski metric:

$$ c^2d\tau^2 = c^2dt^2 - dx^2 - dy^2 - dz^2 $$

In this form it can be used for curved paths, i.e. accelerated motion, but in this case where the paths are straight lines the expression for the proper time between two points $(t_1, x_1, y_1, z_1)$ and $(t_2, x_2, y_2, z_2)$ simplifies to:

$$ c^2 \Delta\tau^2 = c^2 \Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2 $$

where $\Delta t = t_2 - t_1$, $\Delta x = x_2 - x_1$, etc.

Let's do the calculation in the rest frame of the Earth. Suppose the distance to Alpha Centauri is $d$, then in the Earth frame the time taken to get there is $t = d/v$. We'll take the $x$ axis to lie in the Earth to Alpha Centauri direction so that $\Delta x = d$ and $\Delta y = \Delta z = 0$ and $\Delta t = d/v$. Substituting into our equation for the proper time between the start and end points gives:

$$ c^2 \tau^2 = c^2 \left(\frac{d}{v}\right)^2 - d^2 $$

Giving us:

$$ \tau = \sqrt{\left(\frac{d}{v}\right)^2 - \frac{d^2}{c^2}} $$

We can make the significance of this more obvious by rearranging it to give:

$$\begin{align} \tau &= \frac{d}{v} \sqrt{1 - \frac{v^2}{c^2}} \\ &= t \sqrt{1 - \frac{v^2}{c^2}} \end{align}$$

And you should immediately spot this is the same as the equation (1) above for the proper time. This is because in the rest frame of the spaceship the spaceship isn't moving (that's what the rest frame means) so for the spaceship $\Delta x = \Delta y = \Delta z = 0$ and therefore the proper time in the rest frame of the spaceship is just:

$$ \tau = T $$

where $T$ is the trip time as measured by the spaceship's clock. But we already know that:

$$ T = t\sqrt{1 - \frac{v^2}{c^2}} $$

because that's just equation (1) that we started with. Therefore for the spaceship we also get:

$$ \tau = t\sqrt{1 - \frac{v^2}{c^2}} $$

And the two observers both agree that the proper time $\tau$ is the same.

This is an absolutely key result. In relativity the proper time measured along the path between two points in spacetime is an invariant. All observers will agree on its value no matter what their velocities. Indeed, they will agree on the proper time even if they are accelerating.

Answer 3

Measurement of rate of a moving clock is carried out the following way:

Stationary observer in reference frame $S$ (the observer on earth) places the clock $C_1$ at coordinate $x_1$ of his frame and the clock $C_2$ at coordinate $x_2$ of his frame.

Then this observer sends a beam of light from clock $C_1$ towards clock $C_2$. He assumes, that one - way speed of light is c (Einstein synchrony convention). Since he knows distance and speed of light, he synchronizes these clocks, so as they show “the same time” in reference frame $S$.

https://en.wikipedia.org/wiki/Einstein_synchronisation

Then this observer can measure rate of a clock, which moves in his reference frame $S$

Imagine that moving clock (an observer in the spaceship) $C'$ passes by clock $C_1$ at moment of time $t_1$ first and clock $C_2$ at moment of time $t_2$ some later. At these moments, readings of the moving clock and the corresponding fixed clock of reference frame $S$ next to it are compared.

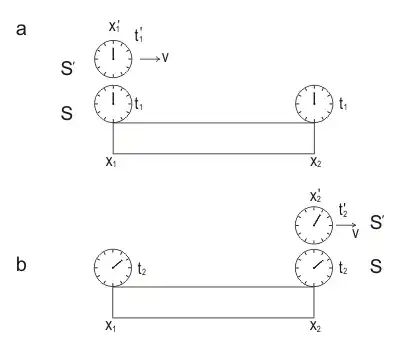
Let the counters of moving clock measure the time interval $\tau _ {0}$ during the movement from the point $x_ {1}$ to the point $x_ {2}$ and the counters of clocks $C_1$ and $C_2$ of the fixed or “rest” frame $S$, will measure the time interval $\tau$. This way,

$$\tau '=\tau _{0} =t'_{2} -t'_{1},$$

$$\tau =t_{2} -t_{1} \quad (1)$$

But according to the inverse Lorentz transformations we have

$$t_{2} -t_{1} ={(t'_{2} -t'_{1} )+{v\over c^{2} } (x'_{2} -x'_{1} )\over \sqrt{1-v^{2} /c^{2} } } \quad (2)$$

Substituting (1) into (2) and noting that the moving clock is always at the same point in the moving reference frame $S'$, that is,

$$x'_{1} =x'_{2} \quad (3)$$

We obtain

$$\tau ={\tau _{0} \over \sqrt{1-v^{2} /c^{2} } } ,\qquad (t_{0} =\tau ') \quad (4) $$

This formula means that the time interval measured by the fixed clocks is greater than the time interval measured by the single moving clock. Time in reference frame S is running $\gamma$ times faster from the point of view of moving clock $C'$. This means that the moving clock lags behind the fixed ones, that is, it slows down.

The animation below depicts the rest frame (a row of synchronized clocks) and the moving clock (single clock).

Chapter: time dilation http://www.pstcc.edu/departments/natural_behavioral_sciences/Web%20Physics/Chapter039.htm

NOTE

Proper time is the time on your wristwatch. However, if you are stationary in the reference frame $S$, all clocks in this reference frame, billions of clocks, let’s say, show the same time (according to SR). These clocks do not move relatively to you.

By means of these clocks you can record time and spatial coordinate of an event (when and where it takes place).

Time is the same in the whole reference frame, or your rest frame.

An observer in SR never admits, that he moves. Every observer is at rest in his own reference frame and all other stuff (clocks, rods etc. ) moves around. Observers in SR change frame. Tom has his own, Ben has his own, Herb has his own etc. It is never mutual.

Thus, an observer in the spaceship does the same trick as the observer on earth. He assumes that he is at rest and the Earth moves. He puts two spatially separated clocks and measures time intervals the same way as the Earthman. That is drawn on the picture below.

I don’t know what to say if these proper times are the same. May be they are rather personal.

Good to note - as soon as an observer assumes, that he is not at rest but he is in moton an certain reference frame, he will see, that all clocks are ticking faster, than his own and measuring rods are longer than his own.