It is a standard result that quantum mechanics does not allow for superluminal communication, which would seem to directly imply that the answer to this question is no. After all, Bell's result tells us about correlations, and we know that correlation does not necessarily imply causation.
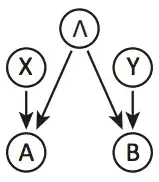
However, if we restrict our attention to solely the measurement outcomes, Bell's theorem also tells us that we cannot think of the observations of Alice and Bob as correlated via a third variable. In other words, it rules out the following causal structure:
More precisely, the result (stated in the CHSH formulation) is that, if there is an underlying probability distribution $p(a,b,x,y,\lambda)$ which is such that (*) $$p(a,b|x,y,\lambda)=p(a|x,\lambda)p(b|y,\lambda),\tag1$$
then some functional relations between the values of $x, y$ and the conditional marginal distribution $p(a,b|x,y)$ are not possible. In other words, (1) imposes restrictions on the following function: $$f(a,b,x,y)\equiv \sum_\lambda p(a,b|x,y,\lambda)p(\lambda)=p(a,b|x,y).\tag2$$ These restrictions are made evident when taking expectation values over all possible outcomes, that is by studying the function $g$ defined as $$g(x,y)\equiv\sum_{a,b}ab \,\,f(a,b,x,y).$$
In particular, it is not possible (and this is the content of CHSH result) to have something like $$g(x,y)=\boldsymbol x\cdot\boldsymbol y.$$
Now let us consider the quantum case. The full probability distribution has to be written in the more general form $p(a,b,x,y)$, and whenever a form of Bell's inequalities is violated by this distribution, then we know that we cannot factorize it with the help of an additional variable as in (2).
However, we can still assume that the measurement setups are chosen independently, so that we can still write $$p(x,y)=p(x)p(y),$$ althought we cannot write $p(a,b,x)=p(a,x)p(b)$ or $p(a,b,y)=p(b,y)p(a)$.
My question is then precisely about these last statements: does the fact that $p(a,b,x)$ cannot be factorized as $p(a,x)p(b)$ imply that there is a causal relation between the two measurement outcomes?
(*)
Eq. (1) can be equivalently stated as a statement about the structure of the full joint probability distribution describing $p(a,b,x,y,\lambda)$ the whole behavior: $$p(a,b,x,y,\lambda)=\frac{p(x,y,\lambda)}{p(x,\lambda)p(y,\lambda)}p(a,x,\lambda)p(b,y,\lambda),$$ where every time a variable is not included as an argument we are talking about the marginal distribution with respect to that variable, so that for example: $$p(a,x,\lambda)\equiv\sum_{b,y}p(a,b,x,y,\lambda).$$