Reverse engineering a time dilation problem

Question

Consider the following problem

A rocket with a clock moves at $0.8c$ relative to the earth. An observer A on the rocket measures a time interval of 6 seconds. With respect to an observer B on the earth, the time interval is $$\frac{6}{\sqrt{1-(0.8)^2}}=10$$ seconds.

I got confused if I reverse engineer the problem as follows. The observer A knows that the observer B will measure 10 seconds. With respect to A, the observer B moves at $0.8c$. The observer A calculates $$\frac{10}{\sqrt{1-(0.8)^2}}=\frac{50}{3}$$ seconds which is not the same as the original one (6 seconds).

Question

What is wrong in my understanding?

Answer 1

You need to use the general form of the Special Relativity Lorentz transforms.

Suppose an observer in frame $S$ measures spacetime coordinates $(ct,x,y,z)$ and an observer in frame $S'$ (which moves at velocity $v$ in frame $S$ along the $x$-axis) measures coordinates $(ct',x',y',z')$. The relationship between these coordinates may be shown to be

\begin{align} ct'&=\gamma(ct-\beta x)\\ x'&=\gamma(x-\beta ct)\\ y'&=y\\ z'&=z \end{align}

where $\gamma = 1/\sqrt{1-\beta^2}$ and $\beta=v/c$.

We can also apply these formulae to intervals in spacetime (between two events, call them $1$ and $2$):

\begin{align} c\Delta t'_{12}&=\gamma(c\Delta t_{12}-\beta \Delta x_{12})\\ \Delta x'_{12}&=\gamma(\Delta x_{12}-\beta c\Delta t_{12})\\ \Delta y'_{12}&=\Delta y_{12}\\ \Delta z'_{12}&=\Delta z_{12} \end{align}

We can also get inverse transformations (going from $S'\rightarrow S$): \begin{align} c\Delta t_{12}&=\gamma(c\Delta t'_{12}+\beta \Delta x'_{12})\\ \Delta x_{12}&=\gamma(\Delta x'_{12}+\beta c\Delta t'_{12})\\ \Delta y_{12}&=\Delta y'_{12}\\ \Delta z_{12}&=\Delta z'_{12} \end{align}

In your example, we have the observer in the "moving" frame (in the rocket) in frame $S'$, and they measure some interval between events $1$ and $2$ in spacetime:

\begin{align} c\Delta t'_{12}&=6c\text{ s}\\ \Delta x'_{12}&=0\\ \Delta y'_{12}&=0\\ \Delta z'_{12}&=0\\\\ \gamma &= \frac{5}{3}\\ \beta &= 0.8 \end{align}

Note that in the rocket's frame, the spatial intervals are all zero, because events $1$ and $2$ happen in the same place (the rocket) in this frame.

Applying the inverse transforms to get $(c\Delta t_{12},\Delta x_{12},\Delta y_{12},\Delta z_{12})$, we obtain: \begin{align} c\Delta t_{12}&=\gamma c\Delta t'_{12} = \frac{6c}{\sqrt{1-0.8^2}} = 10c\text{ s}\\ \Delta x_{12}&=\gamma\beta c\Delta t'_{12} = 0.8c\times\frac{6}{\sqrt{1-0.8^2}} = 8c\text{ s}\\ \Delta y_{12}&=0\\ \Delta z_{12}&=0 \end{align}

Note that the first equation is the same as the answer you've quoted in your question.

Now we can check this is right by converting back... We start with \begin{align} c\Delta t_{12}&=10c\text{ s}\\ \Delta x_{12}&=8c\text{ s}\\ \Delta y_{12}&=0\\ \Delta z_{12}&=0 \end{align}

and sure enough, you'll find you get what you started with: \begin{align} c\Delta t'_{12}&=\gamma(c\Delta t_{12}-\beta \Delta x_{12}) = \frac{5}{3}\times(10c-0.8\times8c) = 6c\text{ s}\\ \Delta x'_{12}&=\gamma(\Delta x_{12}-\beta c\Delta t_{12}) = \frac{5}{3}\times(8c-0.8\times10c) = 0\\ \Delta y'_{12}&=\Delta y_{12}=0\\ \Delta z'_{12}&=\Delta z_{12}=0 \end{align}

The moral here is in general we have to be careful not only when events occur in a given reference frame, but also where in that frame.

The answer you quote is technically correct, but quietly ignores the fact that the events $1$ and $2$ happen at the same place in space in the rocket's frame.

Answer 2

It helps to think geometrically, with a spacetime diagram.
I've drawn one on rotated graph paper so that we can more easily count the tickmarks.

Observer Alice (RED) moves with (4/5)=PQ/OP according to Bob (BLUE). Each light-clock-diamond counts as "2 ticks".

Referring to your original problem, OQ=6 along Alice's worldline has an apparent elapsed time of 10 according to Bob. Bob uses OP on his worldline to measure the elapsed time of OQ on Alice's worldline because Bob says P and Q are simultaneous.
This sets up a right-triangle OPQ in spacetime, with right-angle at P and OQ is the hypotenuse and OP is the adjacent side. Trigonometrically, $$\frac{OP}{OQ}=\frac{\rm adjacent}{\rm hypotenuse}=\cosh\theta,$$ where $\theta$ is the Minkowski-angle between OP and OQ. Physically, $\cosh\theta$ is time-dilation factor $\gamma=\frac{1}{\sqrt{1-v^2}}$. (The velocity is $v=\tanh\theta$.)

Thus, the first equation in your problem is $$OQ\cosh\theta= \stackrel{?}{OP}$$ where you specified the hypotenuse $OQ$ and $v$ (implicitly $\theta$), and the adjacent side $OP$ is unknown.

That is, "What would Bob say is the apparent elapsed time of OQ (the adjacent side of OPQ) , if Alice says OQ=6 (the hypotenuse of OPQ)?"

To "reverse engineer" the problem, you have to use the same triangle OPQ since you are interested in $OQ$. So, by algebra, the reverse engineered equation is $$\stackrel{?}{OQ}= \frac{\stackrel{\checkmark}{OP}}{\cosh\theta}$$

That is, "If Bob knows "the apparent elapsed time of OQ" (as measured using OP, where Bob says P and Q are simultaneous) [the adjacent side] is 10, what would [the hypotenuse] OQ be?"

---

Your error is that you have set up the analogous problem for right-triangle triangle OZP, where Alice is trying the measure the apparent time of OP on Bob's worldline using OZ on her worldline. Alice says Z and P are simultaneous.

That is, "What would Alice say is the apparent elapsed time of OP (the adjacent side of OZP) , if Bob says OP=10 (the hypotenuse of OZP)?"

Answer 3

$\let\D=\Delta \let\g=\gamma$ Your question (and your misunderstanding) is recurring over and over. Your first application of time dilation formula is right, the second is wrong. Why? Simply because some simple points must be kept, referring to reference frames and events.

You have two frames, say A (the rocket) and B (the Earth). Then you think of a clock at rest in frame A measuring an interval of 6 seconds. Time interval between what? Between two events, happening in frame A: starting ($E_1$) and stopping ($E_2$) of the clock.

B observes the same events, but is reckoning their times with two clocks, standing in frame B. Two clocks are needed, since events $E_1$ and $E_2$ do not occur in the same place of B. In this situation it correct to write $$\D t_{\rm B} = \g\,\D t_{\rm A} \tag 1$$ as you did.

Your second calculation instead cannot refer to the same events. It would apply if you were talking of a clock on earth, measuring an interval of 10 s and observed from the rocket. Now events are no longer $E_1$ and $E_2$ but two other, say $F_1$ and $F_2$: start and stop of clock on earth. These events happen in the same place of frame B, but if you want to observe them from A and measure their interval, you need two clocks standing in frame A. Then again you may use time dilation, in reverse: $$\D t'_{\rm A} = \g\,\D t'_{\rm B}.\tag 2$$

I've used $\D t'$ and not $\D t$, because the former intervals, eq. (1), referred to events $E_1$ and $E_2$. Intervals in eq. (2) refer to events $F_1$ and $F_2$ instead.

Answer 4

You try to compare clock A with clock B, it is senseless.

The trick of Special Relativity is that you don't stay within one once chosen frame, but change frames. Each and every observer has his own "personal" frame of reference and thinks that he is "at rest". One frame is not enough and nobody confesses that he can move.

So, it makes no sense to say, that A moves relatively to B or vice versa. It is correct to say, that A moves in the reference frame of B and vice versa.

Reference frame is a lattice of synchronized clocks. Each "stationary" observer attaches to himself this lattice of synchronized clocks to measure space and time coordinates of events.

It is very important to understand method of synchronization of these clocks. Special relativity fantasizes that one - way speed of light is isotropic in all frames and allows only method to synchronize clocks - Einstein synchronization. This synchronization keeps one - way speed of light isotropic.

It works like that: person flashes a flash and when light reaches certain clock, adjusts this clock, assuming that one - way speed of light is c in all directions.

However, there are others self - consistent synchronizations. Einstein synchronization is a special case of Reichenbach's synchronization. Reichenbach's synchronization allows anisotropic one way speed of light, while two - way speed of light is isotropic.

For example, according to Reichenbach, speed of light in one direction can be very close to c/2 and in the other infinitely large, so two - way speed will still be c.

So, the time dilation formula means:

Single clock $S$ ticks slower than all Einstein - synchronized clocks of reference frame of $S'$; that means that according to clock $S$, time in reference frame $S'$ flows $1/\sqrt {1-v^2/c^2}$ times faster.

Single clock $S'$ ticks slower than all Einstein - synchronized clocks of reference frame of $S$; that means that according to clock $S'$, time in reference frame $S$ flows $1/\sqrt {1-v^2/c^2}$ times faster.

That goes out straight from the Lorentz transformations. We can take only two Einstein - synchronized clocks of "resting" reference frame $S$ or $S'$.

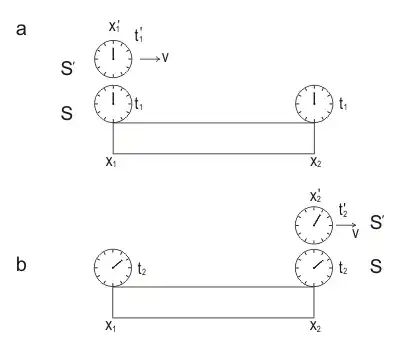
We can demonstrate time dilation of the SR in the following experiment (Fig. 1). Moving with velocity $v$ clocks measure time $t'$. The clock passes past point $x_{1}$ at moment of time $t_{1}$ and passing past point $x_{2}$ at moment of time $t_{2}$.

At these moments, the positions of the hands of the moving clock and the corresponding fixed clock next to it are compared.

Let the arrows of moving clocks measure the time interval $\tau _ {0}$ during the movement from the point $x_ {1}$ to the point $x_ {2}$ and the hands of clocks 1 and 2, previously synchronized in the fixed or “rest” frame $S$, will measure the time interval $\tau$. This way,

$$\tau '=\tau _{0} =t'_{2} -t'_{1},$$

$$\tau =t_{2} -t_{1} \quad (1)$$

But according to the inverse Lorentz transformations we have

$$t_{2} -t_{1} ={(t'_{2} -t'_{1} )+{v\over c^{2} } (x'_{2} -x'_{1} )\over \sqrt{1-v^{2} /c^{2} } } \quad (2)$$

Substituting (1) into (2) and noting that the moving clock is always at the same point in the moving reference frame $S'$, that is,

$$x'_{1} =x'_{2} \quad (3)$$

We obtain

$$\tau ={\tau _{0} \over \sqrt{1-v^{2} /c^{2} } } ,\qquad (t_{0} =\tau ') \quad (4) $$

This formula means that the time interval measured by the fixed clocks is greater than the time interval measured by the single moving clock. This means that the moving clock lags behind the fixed ones, that is, it slows down.

So, from the “point of view" of the "moving" single clock $S'$, time in reference frame $S$ flows $\gamma$ times faster.

This way we can see, that if moving observer compares his clock readings successively with synchronized clocks of reference frame he moves in, he will see, that these clocks change readings $\gamma$ times faster.

The animation below vividly demonstrates change of frames and "reciprocal" time dilation:

However, critical analysis of relativistic Doppler shift formula shows, that "A is slower than B and B is slower than A" is hardly possible.

Let's turn to the celebrated A. Einstein’s work “On the Electrodynamics of Moving Bodies”, &7, Theory of Doppler Principle and Aberration:

http://hermes.ffn.ub.es/luisnavarro/nuevo_maletin/Einstein_1905_relativity.pdf

From the equation for $\omega$ it follows that if an observer is moving with velocity $v$ relatively to an infinitely distant source of light of frequency $\nu$, in such a way that the connecting line “source-observer” makes the angle $\phi$ with the velocity of the observer referred to a system of co-ordinates which is at rest relatively to the source of light, the frequency $\nu'$ of the light perceived by the observer is given by the equation

$$\nu'=\nu \frac {1-cos \phi \cdot v/c}{\sqrt {1-v^2/c^2}} \quad (5)$$

Mr. Einstein clearly speaks that an observer is moving with velocity $v$ and that "the velocity of the observer referred to a system of co-ordinates which is at rest relatively to the source of light"

It is clear, that at the moment when "the connecting line “source-observer” makes the angle $\pi/2$ with the velocity of the observer" the formula (5) reduces to:

$$\nu'=\frac {\nu}{\sqrt {1-v^2/c^2}} \quad(6)$$

This is Transverse Doppler effect in the frame of the source. According to Mr. Einstein, when moving observer is at points of closest approach to the source, he sees only contribution of time dilation into relativistic Doppler shift (his clock is running slower), so the clock "at rest" appears to him running $\gamma$ times faster.

That simply means, that "A is slower that B" (Einstein synchronization) and "B is faster than A" (Reichenbach synchronization) is self - consistent, if A is considered "moving" and B is "at rest"

Please find transverse Doppler Effect diagram below:

Some references:

https://en.wikipedia.org/wiki/Observer_(special_relativity)

https://en.wikipedia.org/wiki/One-way_speed_of_light

https://en.wikipedia.org/wiki/Einstein_synchronisation

Relativistic Doppler Effect in Feynman Lectures and Mathpages/ http://www.feynmanlectures.caltech.edu/I_34.html https://www.mathpages.com/home/kmath587/kmath587.htm