3

Is "more added heat, more molecular vibration" an universal property? Or are there exceptions?

Do some substances work the other way around? Or do some other ambient properties modify this property? Such as if the substance is applied electrical current at the same time? Or e.g. submerged to some other substance?

mavavilj
  • 459

3 Answers3

3

No. Consider a phase transition. This requires heat, but the temperature stays the same. So classically, the kinetic energy would remain the same.

And then there are spin systems where there is no movement, so it is not universal.

Adding heat $Q$ means adding entropy $S$: ${\rm d}S = \delta Q/T$.

  • In a phase transition, even though the temperature stays the same, the ratio of the different phases does not, and you claim that the kinetic energy remains the same. Is that really correct? – untreated_paramediensis_karnik Oct 21 '18 at 14:23
  • 1
    @coniferous_smellerULPBG-W8ZgjR In the melting of for example lead, the ratio solid/liquid changes from 1 to 0 while the temperature stays constant. Such heavy atoms behave classically at such temperatures, so the kinetic energies should remain the same. This is not true when zero-point motion most be taken into account, as for example for the protons in ice or water. There are measurements by Fradkin of solid and liquid argon: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.49.3197 –  Oct 21 '18 at 14:42
1

In addition to Pieter's answer which claims that during a phase transition adding more heat does not contribute to a change in kinetic energy, I add that in some phase transitions, adding more heat converts a liquid to a solid, thereby lowering the kinetic energy of the molecules.

I am not sure I agree with Pieter's answer, because I'd argue that even though the temperature stays the same during a phase transition, if liquid is converted to gas or solid is converted to either liquid or gas, the kinetic energy of the molecules do increase.

Edit: As requested by Pieter, a concrete example of a liquid material that becomes a solid when heat is added is helium 3. See the corresponding phase diagram: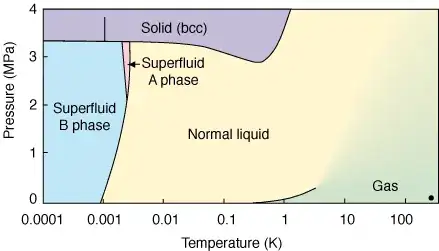

Note that it isn't the only substance having this property. I do not remember the exact name of such substances, but I do remember a good thermoelectric one having that property too.

untreated_paramediensis_karnik
  • 6,039
  • In what system does adding more heat convert a liquid to a solid? –  Oct 21 '18 at 14:57
  • @Pieter See my edit. I was at a conference a few days ago and someone showed a phase diagram of a material having that property. Unfortunately I do not remember the exact name of the material, the chemical formula wasn't simple. – untreated_paramediensis_karnik Oct 21 '18 at 18:35
  • 1
    Helium is of course a quantum liquid and a nice answer to the OP question of things maybe being the other way around. All that I claimed is that classically the kinetic energy is the same for both phases at the transition temperature. That is not general at all. Not even for ice and water: the zero-point energy of the protons change things. –  Oct 21 '18 at 19:34
-1

For a system of molecules always $T\geq0$. With the standard definition of temperature as a number proportional to the average energy in the degrees of freedom of a system, always $T\geq0$. For more exotic systems, it depends on how you define temperature. You can define temperature as the inverse rate of increase of entropy with energy, that is $T=\left( \frac{dS}{dE}\right)^{-1}$. With this definition negative temperature is possible. Examples are give here.

my2cts
  • 24,097
  • That is not the standard definition of temperature. And the question was not about temperature. –  Oct 20 '18 at 10:31
  • The question is about heat, which is energy flowing between systems of different temperature. You can't discuss heat without discussing temperature. Moreover, I explicitly stated that this was a diferent definition form standard. Any other questions, @Pieter ? – my2cts Oct 20 '18 at 10:35
  • You state that in the standard definition, temperature is proportional to the average energy in the degrees of freedom. That is totally wrong. And of course one can talk about adding heat without mentioning temperatures. Resistive heating, friction, etc. –  Oct 20 '18 at 10:39
  • @Pieter Strong statements require solid back up: how is the energy equipartition theorem ( https://en.wikipedia.org/wiki/Equipartition_theorem ) wrong ? Is $ \neq k_B T/2$ per degree of freedom? And how are your discussions of heat going without mentioning temperature? What are your statements based on? – my2cts Oct 20 '18 at 10:56
  • Equipartition leads to constant $c_p$, contradicting the third law of thermodynamics. It is more the definition of degree of freedom, it cannot define temperature. And just a minute ago I was boiling water, supplying heat electrically from the mains. –  Oct 20 '18 at 11:03
  • @Pieter All links and texts I have seen on the equipartition theorem claim that it leads to a definition of T related to the average energy per DoF. I do not see any reference to the objections that you have against this. If you have references that all of this wrong, bring 'em out. By the way, your mains did not deliver heat but electronic kinetic energy. – my2cts Oct 20 '18 at 11:15
  • Let us continue this discussion in chat. –  Oct 20 '18 at 17:48